planimetria. enigma: Dany jest trapez ABCD o kącie prostym przy wierzcholkach A i D. Ramie pochyle ma długość 6, a krótsza podstawa 4. Wyznacz długość ramienia prostopadlego i drugiej podstawy, wiedząc, że w ten trapez można wpisac okrąg.

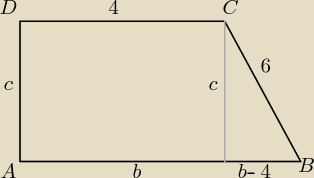
Godzio: 4 + b = 6 + c c² + (b−4)² = 36 c = b − 2 (b−2)² + b² − 8b + 16 = 36 b² + 4b + 4 + b² − 8b − 20 = 0 2b² − 4b − 16 = 0 b² − 2b − 8 = 0 Δ = ... √Δ = ... b₁ = ... b₂ = ... −> ujemny wynik odrzuć c = b − 2 dokończ

Svanar: bajka

Godzio: żeby tylko takie zadania na maturce nie ?

Svanar: sama przyjemnosc by byla

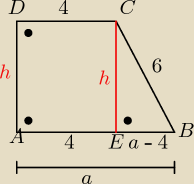
kos: z warunku opisania trapezu na okregu: h+6= a+4 => h= a −2 IEBI= a −4 z tw. Pitagorasa w ΔEBC: (a−2)² + (a−4)² = 6² wyznacz a, pamiętając ,że a >0 i h>0

kos: Godzio popraw błąd! b²−4b +4 +............. równanie ostateczne ; b² −6b −8=0

kos:

Godzio: no tak b² − 4b + 4 + b² − 8b − 20 = 0 2b² − 12b − 16 = 0 b² − 6b − 8 = 0 i dalej już wiadomo

kos: