trójkąt opisany na kole angelika: Na kole o promieniu 2 opisano trójkąt prostokątny o przyprostokątnym długości x i y. Wyznacz funkcję zmiennej x opisującą długość boku y. Określ dziedzinę tej funkcji i naszkicuj jej wykres.

Rumpfy:

Amaz: a znasz wynik?

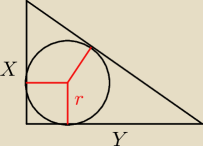
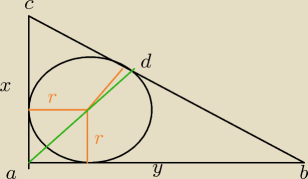
Spike: Najpierw pytanie: wysokość poprowadzona w trójkącie prostokątnym z wierzchołka z kątem prostym będzie przechodzić przez środek okręgu wpisanego w ten trójkąt? Właśnie tego nie jestem pewien, i dlatego wynik może być zły. Rysunek trochę niedokładny. Może coś takiego r=2 skoro tak, to masz kwadrat o boku 2 zaznaczony na pomarańczowo, jego przekątna to 2√2. Cały zielony odcinek to przekątna kwadratu i promień, więc 2+2√2. Przekątna jest nachylona do x i y pod kątem α=45* Pole trójkąta to

	1
P=		xy
	2

Jest również równe sumie pól trójkątów abd + adc

	1		1		1		√2
P=		*sin45*x*(2+2√2)+		*sin45*y*(2+2√2)=		*		*(2+2√2)(x+y)
	2		2		2		2

Przyrównujesz to teraz

1		1		√2
	xy=		*		*(2+2√2)(x+y)
2		2		2

xy=(√2+2)(x+y)

xy
	=x+y
√2+2

x
	*y−y=x
√2+2

	x
y(		−1)=x
	√2+2

	x−√2−2
y(		)=x
	√2+2

	√2+2
y=x*
	x−√2−2

Spike: Tylko, że jest to oparte o to założenie, a nie wiem czy jest słuszne.

Wydi: proponuje zajrzeć http://matematyka.pl/190385.htm SPIKE wysokość nie przechodzi przez środek okręgu!

Wydi:

Spike: Hmm, cytat teraz "Okrąg wpisany w trójkąt. Środek takiego okręgu znajduje się w przecięciu dwusiecznych kątów wewnętrznych trójkąta." To by wychodziło, że dla prostokątnego jest to prawda.

Wydi: Zobacz, że Twój okrąg wcale nie jest okrągły Raczej się mylisz...co do wysokości

Spike: Wiesz na czym błąd w moim myśleniu polegał? Trójkąt prostokątny równoramienny, tyle powiem

Wydi: Dobrze że do tego doszedłeś Na pewno nie w prostokątnym. Pozdrawiam!

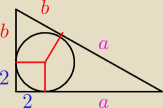GrAbArZ: Patrzac na date pewnie moja pomoc nie wiele sie przyda ale jak juz rozwiazalem to napisze (a+2)²+(b+2)²=(b+a)² x=2+b => b=x−2 y=2+a => a=y−2 w pierwszym redukujemy ile sie mozna podstawiamy zmienne wyciagamy to co trzeba i koniec zadanka

monialisia: a jak to dalej pociągnąć? w sensie od 4a+4b+8=2ab, chyba, że coś pokręciłam i teraz nwm