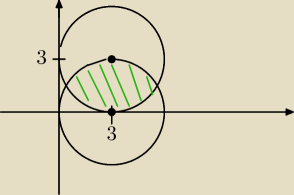
 oblicz pole części wspólnej okręgów o równaniach
(x−0)2 + (y−3)2 = 9
(x−3)2 + (y−3)2 = 9
oblicz pole części wspólnej okręgów o równaniach
(x−0)2 + (y−3)2 = 9
(x−3)2 + (y−3)2 = 9



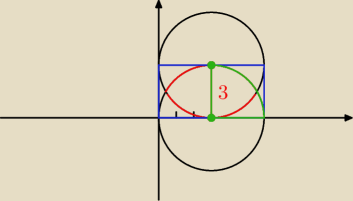 niebieskie => prostokąt −> P = 3 * 6 = 18
niebieskie => prostokąt −> P = 3 * 6 = 18
| 1 | 9 | |||
zielone => wycinek koła −> P = | π*9 = | π | ||
| 4 | 4 |
| 1 | ||
jeżeli od jednego z kwadratów o polu 3*3 odejmiemy | pola koła to otrzymamy jeden z dwóch | |
| 4 |
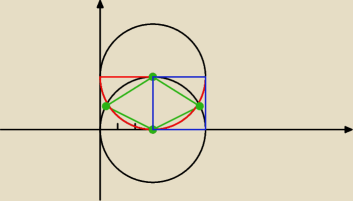
| 9√3 | ||
Pkwadratu − Ptrójkąta = 9 − | ||
| 4 |
| 9√3 | 9√3 | 9√3 | ||||
Pprostokąta − 2 * ( 9 − | ) = 18 − 18 + | = | ||||
| 4 | 2 | 2 |
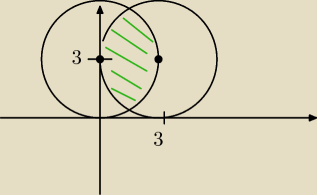 masz rację Lothar. tak powinien wyglądac rysunek
masz rację Lothar. tak powinien wyglądac rysunek  ale wynik będzie ten sam
ale wynik będzie ten sam
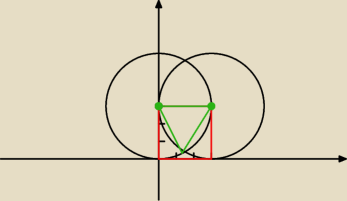 nie popatrzyłem na równania tylko na rysunek koleżanki ...
Rozwiązanie będzie identyczne
nie popatrzyłem na równania tylko na rysunek koleżanki ...
Rozwiązanie będzie identyczne

 Nie dobra poddaje się znów został ten skrawek, jeszcze nad tym pomyśle
Nie dobra poddaje się znów został ten skrawek, jeszcze nad tym pomyśle 
 ok
ok
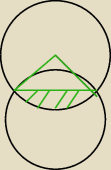 pole całego zielonego obszaru łatwo obliczyć poleWycinaKola=alfa/360 * pole koła, gdzie alfa to
kąt trójkąta w wierzchołku znajdującym się w środku koła, pole zakreskowanego obszaru to
poleWycinakKola − poleTrójkątaZielonegoPustego w ten sposób obliczyliśmy część dolnego,
wspólnego obszaru kół zakreskowaną na zieloną, teraz to samo trzeba zrobić dla części górnej
pole całego zielonego obszaru łatwo obliczyć poleWycinaKola=alfa/360 * pole koła, gdzie alfa to
kąt trójkąta w wierzchołku znajdującym się w środku koła, pole zakreskowanego obszaru to
poleWycinakKola − poleTrójkątaZielonegoPustego w ten sposób obliczyliśmy część dolnego,
wspólnego obszaru kół zakreskowaną na zieloną, teraz to samo trzeba zrobić dla części górnej