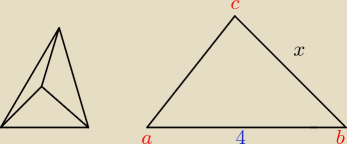
Podstawą ostrosłupa jest trójkąt, którego jeden bok ma długość 4, a kąty przyległe do tego boku
mają miary 75 i 45 stopni. Wysokość ostrosłupa ma długość równą długości promienia koła
opisanego na podstawie. Oblicz objętość.
1. rysunek podstawy jest mój, wiec może być zle
jeśli ktoś moze sprawdzić, i policzyć V..... bo mi zawsze źle wychodzi :x
wiec z danych wynika:
∠A = 45stopni
∠B=75stopni
∠C=180−(45+75)=180−120=60
oraz R=H
wiec liczymy:
| 4 | |
= R | |
| 2sin60 |
| 2 | 4 | 4√3 | ||||||||||
R= | = | = | = H | |||||||||
| √3 | 3 |
| 4 | x | 4sin45 | |||
= | → x= | ||||
| sin60 | sin45 | sin60 |
| 4√6 | ||||||||||||
X= | = | = 2√6 | |||||||||||
| 2 |
| 16 | 16 | |||
V= | + | √3 | ||
| 6 | 9 |
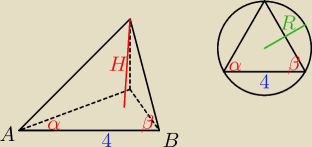bez wlasnego rys nie moge nawet myslec 
takie skrzywienie 
żeby tylko wynik dobry wyszedł ja liczyłem 2 razy i nic, zawsze licznik
zawodzi 
| 4√6 | ||
x = | ||
| 3 |
| 1 | sinβ * sinγ | |||
P{Δ} = | a2 * | = 2R2 * sinβ * sinγ * sinα
| ||
| 2 | sinα |
| √2 | ||
sinα = sin45 = | ||
| 2 |
| √6 + √2 | ||
sinβ = sin75 = sin (30 + 45) = | ||
| 4 |
| √3 | ||
sinγ = sin60 = | ||
| 2 |
| 3 + √3 | ||
P{Δ} = | = 2R2 * sinβ * sinγ * sinα
| |
| 3 |
| 3 + √3 | 3 + √3 | ||
= R2 * | |||
| 3 | 4 |
| 2 | ||
R = H = | ||
| √3 |
| 1 | 1 | 3 + √3 | 2 | |||||
V = | * Pp * H = | * | * | =
| ||||
| 3 | 3 | 3 | √3 |
dzieki a sprawdzałem po 2 razy każde obliczenie....
| √6 + √2 | ||
sin75 = sin(30+45) = wzór ... = | ||
| 4 |
| 1 | 1 | √6 + √2 | 4√6 | |||||
Pp = | * sin75 * x * 4 = | * | * | * 4 = | ||||
| 2 | 2 | 4 | 3 |
| 2√6 | 12 + 4√3 | |||
(√6 + √2) * | = | |||
| 3 | 3 |
| 1 | 4√3 | 12 + 4√3 | 16 + 16√3 | |||||
V = | * Pp * H = | * | = | |||||
| 3 | 9 | 3 | 9 |
| 2√3 + 2 | ||
mi wyszlo | ... | |
| 9 |
| 1 | ||
Pp = | * sinα*a*b jest taki wzór w tym wypadku | |
| 2 |
| 1 | ||
Pp = | *sin75 * x * 4 dalej podstawiasz i wyliczasz | |
| 2 |