Czworokąt wypukły. Keisim: Dany jest taki czworokąt wypukły ABCD, że okręgi wpisane w trójkąty ABC i ADC są styczne. Wykaż, że w czworokąt ABCD można wpisać okrąg. Jak znam życie, trzeba w jakiś sposób wykazać, że suma przeciwległych boków jest równa? Zbija mnie z tropu to, że okręgi są styczne... znaczy to, że promienie poprowadzone do przekątnej tych małych okręgów wpisanych są prostopadłe do niej. Czy taka sytuacja może zajść w innym przypadku niż romb?

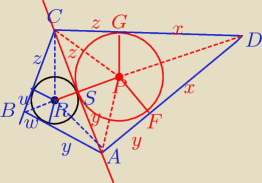
Basia: ten rysunek to cały dowód no należy uzasadnić, że tr.PFD i tr.PGD są przystające itd. parami

Keisim: Deltoid... Dziękuję Basiu, jesteś wielka. Z uzasadnieniem sobie już poradzę...

Basia: to nie musi być deltoid; tak mi wyszło na rysunku, ale nie musi AB=w+y BC=w+z CD=z+x AD=x+y stąd AB+CD=x+y+w+z BC+AD=x+y+w+z

Eta: widzę ,że już mam z "głowy" Zanim zrobiłam herbatkę , Basia ..... roztrzaskała rysunek

Keisim: Faktycznie, dziękuję za uwagę... Zamiast przeanalizować od początku do końca to zadanie, ja zacząłem robić kolejne...