geometria analityczna
Agula: geometria:
W równoramiennym trójkącie prostokątnym punkt C=(3,−1) jest wierzchołkiem kąta prostego.
Przeciwprostokątna trójkąta zawiera się w prostej 3x−y+2=0. Wyznacz pozostałe wierzchołki tego
trójkąta.
1 maj 14:47
Basia:
3x−y+2=0
y=3x+2
A(xa,3xa+2)
B(xb,3xb+2)
AC→ ⊥ BC→
AC→=[3−xa,−1−3xa−2]=[3−xa,−3−3xa]
BC→=[3−xb,−1−3xb−2]=[3−xb,−3−3xb]
|AC→|=|BC→|
(3−xa)2+(−3−3xa)2=(3−xb)2+(−3−3xb)2
9−6xa+xa2+9+18xa+9xa2 =9−6xb+xb2+9+18xb+9xb2
10xa2+12xa=10xb2+12xb
10(xa2−xb2)+12(xa−xb)=0 /:2
5(xa−xb)(xa+xb)+6(xa−xb)=0
(xa−xb)(5xa+5xb+6)=0
xb=xa
lub
5xb=−5xa−6
xb=−xa−65
iloczyn skalarny AC→ i BC→ musi =0
(3−xa)(3−xb)+(−3−3xa)(−3−3xb)=0
(3−xa)(3−xb)+9(1+xa)(1+xb)=0
1.
xb=xa
(3−xa)2+(1+xa)2=0
i trzeba to rozwiązać
2.
(3−xa)(3+xa+65)+9(1+xa)(1−xa−65)=0
i trzeba to rozwiązać
sporo liczenia, ale wyjdą zwykłe równania kwadratowe
możliwe, że jest jakiś prostszy sposób, ale na razie nie mam pomysłu
1 maj 15:22
Agula:
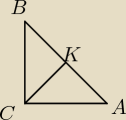
jak ja sobie to probowalam rozwiazac to doszlam do tego, że K=(−
35,
15)
i prosta CK ma równanie y=−
13x
x
A+x
B=−{6}{5}
no i dalej ugrzazlam, wolalabym jakies rozwiazanie bez wektorow bo nie bardzo je rozumiem
1 maj 16:19
Svanar: w sumie, jest chyba inny sposób, ale tez liczenia....
jak masz uzalezniony xa od xb i ya od yb to mozesz próbować ze wzoru:
h2 = P{|BK|*|KA|}
ale tutaj tez bardzo duzo liczenia
1 maj 16:22
Svanar:
H=√Bk*KA ← pomyłka we wzorze
1 maj 16:23
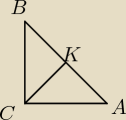 jak ja sobie to probowalam rozwiazac to doszlam do tego, że K=(−35,15)
i prosta CK ma równanie y=−13x
xA+xB=−{6}{5}
no i dalej ugrzazlam, wolalabym jakies rozwiazanie bez wektorow bo nie bardzo je rozumiem
jak ja sobie to probowalam rozwiazac to doszlam do tego, że K=(−35,15)
i prosta CK ma równanie y=−13x
xA+xB=−{6}{5}
no i dalej ugrzazlam, wolalabym jakies rozwiazanie bez wektorow bo nie bardzo je rozumiem