czworościan formeny przecięty płaszczyzną. oblicz długości boków?
angelika: Czworościan foremny przecięto płaszczyzną przechodzącą przez jeden z wierzchołków podstawy i
środki
dwóch krawędzi. Jako przekrój otrzymano trójkąt o polu √11 . Wyznacz dł. krawędzi
czworościanu ?
1 maj 12:56
Rumpfy:
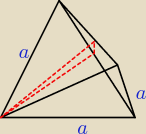
1 maj 13:11
angelika: no własnie tylko co dalej

1 maj 13:15
Rumpfy: tak sobie narysowalem, bo bez rys nie wykombinuje

Czy kat miedzy wysokoscia trojkata czerownego, a wysokoscia tego trojkata zawierajacego
podstawe jest prosty?
1 maj 13:16
Rumpfy: | | a√3 | |
H trojkata w czworosianie = |
|
|
| | 2 | |
Z talesa:
2b = a
| | a√3 | | a√3 | |
H2 + ( |
| )2 = ( |
| )2
|
| | 4 | | 2 | |
| | 3a2 | | 3a2 | | 9a2 | |
H2 = |
| − |
| = |
|
|
| | 4 | | 16 | | 16 | |
P
przekroju =
√11
| | 1 | | a | | 3a | | 3a2 | |
√11 = |
| * |
| * |
| = |
|
|
| | 2 | | 2 | | 4 | | 16 | |
a =
1 maj 13:29
Rumpfy: to jest chyba zle. ;[
1 maj 13:30
angelika: jeszcze myślalam o tym ze h przekroju to a
√3/2
wiec :
√11 =1/2*a/2 *h
√11 = a/4 * h
4
√11 = ah
h= 4
√11 /a
no ale co dalej

1 maj 13:39
Godzio:
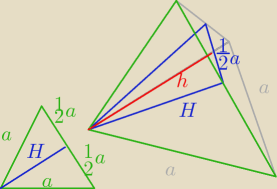
| | | | √11a | | 1 | | 1 | | √11a2 | |
P = |
| = |
| * |
| a * |
| = |
| = √11 /:√11 |
| | 2 | | 4 | | 2 | | 2 | | 16 | |
a
2 = 16
a = 4
1 maj 13:41
angelika: o super! dzieki wielkie

1 maj 13:49


 Czy kat miedzy wysokoscia trojkata czerownego, a wysokoscia tego trojkata zawierajacego
podstawe jest prosty?
Czy kat miedzy wysokoscia trojkata czerownego, a wysokoscia tego trojkata zawierajacego
podstawe jest prosty?


