sin(90' - α) można zapisać jako cos(-α)? Kasia: sin(90stopni − α) można zapisać jako cos(−α)? Zakładając, że to jest dobrze: i potem w zadaniu trafi się na taki przykład:

sinα
	to jak z tego wybrnąć?
cos(−α)

Amaz: sin(90−α)=cosα=cos(−α), to jest dokładnie to samo, nie wiem po co utrudniać sobie życie z tym minusem

Kasia: W sumie jak jest to w równaniu to można podnieść do kwadratu i wtedy z cos(−α) zrobi się cos²α i wszystko.

Kasia: A, to dziękuję! Dla nowicjusza to nie jest taka oczywistość

Amaz: No jest troszke inaczej, bo minus w tym miejscu cos(−x) a w tym: −cosx znaczy całkiem coś innego, lepiej pokaż treść zadania

Kasia: W trójkącie prostokątnym ABC wysokość BD dzieli przeciwprostokątną AC na odcinki o długościach |AD | = 3 i |DC | = 24 . * Oblicz długości boków trójkąta ABC. zastosowałam wzór:

24		3		27
	+		=
sin(90−α)		sinα		sin90

po uproszczeniu:

8		1
	+		= 9
cosα		sinα

Kasia: W odpowiedziach zupelnie inny sposob, nie wiem nawet czy to powyzsze to nie jakieś herezje. Jak uważacie?

Amaz: No troche dziwny sposób, kurde jestem troche zajety teraz, ale zaraz sprawdzę czy to dobrze

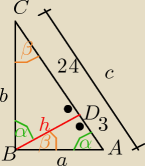
wilga: c= 27 ΔBAD ~ ΔBDC tO

	h		24
		=		=> h2= 3*24= 72
	3		h

z trojkątów prostokątnych : ABD i BDC z tw. Pitagorasa : IABI²= h²+3²= 72+9= 81 => IABI=a= 9 i IBCI²= h²+24²= 648 => IBCI=b= 18√2

Amaz: Dobra ja bym to zrobił inaczej, postaram się zrobić rysunek do tego, myślę, że zajmie mi to z 5minut Jeśli chcesz to poczekaj, jeśli nie to trudno

Amaz: O widzę, że nie muszę robić, chciałem zrobić to podobnie

Kasia: Solidna robota

wilga: