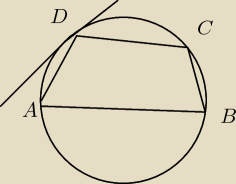
Obliczyć miary kątów w czworokącie wpisanym w okrąg. Xipe: Bok AB czworokąta ABCD wpisanego w okrąg jest średnica tego okręgu. W punkcie D poprowadzono styczna l do tego okręgu, która tworzy z bokami AD i DC katy ostre odpowiednio o miarach 20 i 30. Oblicz miary katów wewnętrznych czworokąta ABCD.

Basia: Xipe zajrzyj do zadania z prawdopodobieństwa, tam był mały błąd wpisałam poprawkę

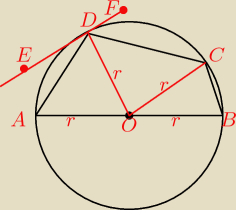Basia: ∡ODE=90 ∡ADE=20 ∡ADO = ∡ODE−∡ADE=70 tr.AOD jest równoramienny ∡OAD=∡ADO=70 [N[α=70] ∡AOD=180−140=40 ∡ODF=90 ∡CDF=30 ∡ODC=90−30=60 δ=70+60=130 tr.DOC jest równoramienny ∡OCD=∡ODC=60 ⇒ ∡COD=60 ∡BOC=180−∡AOD−∡DOC=180−40−60=80 tr.BOC jest równoramienny ⇒

	180−80
∡OBC=∡OCB=		=50
	2

β=50 γ=360−α−β−δ=360−70−50−130=110