| Isin2xI | ||
Naszkicuj wykres funkcji y= | w przedziale (−2pi;2pi) i rozwiąż | |
| sin2x |
| Isin2xI | ||
nierówność | <0 | |
| sin2x |
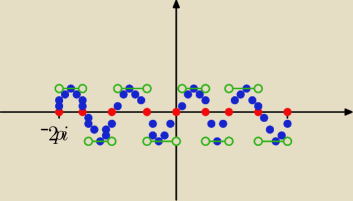 to niebiesko−czerwoneto jest "π razy drzwi" wykres y=sin2x
x∊(−2π,−3π2)∪(−π,−π2)∪(0,π2)∪(π,3π2) ⇒
sin2x>0 ⇒ |sin2x|=sin2x ⇒ f(x)=1>0
x∊(−3π2,−π)∪(−π2,0)∪(π2,π)∪(3π2,2π) ⇒
sin2x<0 ⇒ |sin2x|=−sin2x ⇒ f(x)=−1<0
wykres f(x) to to zielone
to niebiesko−czerwoneto jest "π razy drzwi" wykres y=sin2x
x∊(−2π,−3π2)∪(−π,−π2)∪(0,π2)∪(π,3π2) ⇒
sin2x>0 ⇒ |sin2x|=sin2x ⇒ f(x)=1>0
x∊(−3π2,−π)∪(−π2,0)∪(π2,π)∪(3π2,2π) ⇒
sin2x<0 ⇒ |sin2x|=−sin2x ⇒ f(x)=−1<0
wykres f(x) to to zielone
 , i jeszcze jedno pytanko...
Jak najlepiej rysować ten wykres po kolei?
, i jeszcze jedno pytanko...
Jak najlepiej rysować ten wykres po kolei?
| sin2x | ||
A jeśli ten wykres miałby być w liczniku bez modułu to wykres byłby y= | czy y=1 | |
| sin2x |


 ja tak zrobilem na poczatku
ja tak zrobilem na poczatku