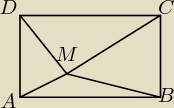
 Punkt M leży wewnątrz prostokąta ABCD. Udowodnij, że
[AM]2+[CM]2=[BM]2+[DM]2
Punkt M leży wewnątrz prostokąta ABCD. Udowodnij, że
[AM]2+[CM]2=[BM]2+[DM]2

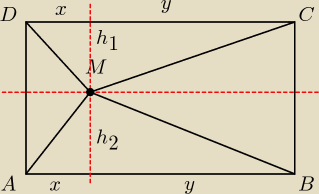 Niech M będzie dowolnym punktem wewnątrz prostokąta. Z tw Pitagorasa mamy:
|DM|2=x2+h12
|BM|2=h22+y2
|AM|2=h22+x2
|CM|2=h12+y2
Dodając stronami mamy równość:
|DM|2+|BM|2=x2+h12+h22+y2
|AM|2+|CM|2=h22+x2+h12+y2
czyli |DM|2+|BM|2=AM|2+|CM|2
Niech M będzie dowolnym punktem wewnątrz prostokąta. Z tw Pitagorasa mamy:
|DM|2=x2+h12
|BM|2=h22+y2
|AM|2=h22+x2
|CM|2=h12+y2
Dodając stronami mamy równość:
|DM|2+|BM|2=x2+h12+h22+y2
|AM|2+|CM|2=h22+x2+h12+y2
czyli |DM|2+|BM|2=AM|2+|CM|2