Stereometria Paweł: Witam serdecznie : ) przygotowuje sie do egzaminu maturalnego i mam problem z jednym zadaniem, Krawędź podstawy ostrosłupa prawidłowego trójkątnego jest równa 6a, cosinus kąta między sąsiednimi ścianami bocznymi tego ostrosłupa jest równy 7/32 . Wyznacz stosunek długości krawędzi bocznej do krawędzi podstawy. I Prośba czy mógłby ktoś narysować o który kąt chodzi? Oraz, z poza zadania, kiedy wiadomo że płaszczyzna przekroju nachylona pod kątem α do podstawy w ostrosłupie bądź graniastosłupie jest trójkątem a kiedy trapezem?

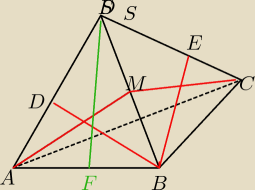
Basia: BD,AM wysokości ASB BE,CM wysokości ASC BD=AM=BE=CM=h kąt, o którym mowa to ∡AMC z tw.cosinisów (6a)²=h²+h²−2h*h*⁷₃₂ 36a²=2h²(1−⁷₃₂) 36a²=2h²*²⁵₃₂ 36a²=h²*²⁵₁₆ h²=36a²*¹⁶₂₅ h=6a*⁴₅=^24a₅ z tw.Pitagorasa AD²+BD²=AB² AD²=36a²−^24*24a2_25*25 AD² = a²*^{36*25*25−24*24}₂₅{25} AD²=a²u(22500−576}{25²} AD²=a²*²¹⁹²⁴_25²

	6√609
AD = a*
	5

SF wysokość ASB tr.ADB ~ tr.AFS ^AD_AF=^AB_AS=^DB_FS ^AD_3a=^6a_b ^b_6a=^3a_AD

	3a
b6a =
	6√609   a*   5

	5		5√609
b6a=		=
	2√609		2*609

nie gwarantuję, że nie ma tam jakiegoś błędu w rachunkach, bo wynik paskudny

Basia: ad. przekroje trudno to wytłumaczyć dysponując dwoma wymiarami spróbuję narysować, ale nie wiem czy Ci to wystarczy

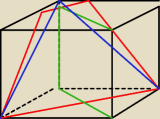
Basia: czerwone trapez, zielone prostokąt, niebieskie trójkąt w graniastosłupie będzie mniej wiecej tak: płaszczyzna prostopadła do podstawy ⇒ prostokąt płaszczyzna nie jest prostopadła do podstawy ⇒ trapez lub trójkąt w ostrosłupach nie da się tego za bardzo usystematyzować, bo to zależy i od kształtu podstawy i od tego czy ostrosłup jest prawidłowy wydaje mi się, że każdy przypadek należy rozpatrywać indywidualnie

Basia: oczywiście jest tak błąd w rachunkach, ale łatwy do poprawienia w końcówce AD nie 5 tylko 25; przeoczyłam, że jest 25²

Paweł: Dziękuje Pani bardzo, i podziwiam Panią za poświęcenie tyle czasu jednej osobie : ) Jeśli jest jakaś możliwość odwdzięczenia proszę napisać ; )