Problem - wyjaśnijcie mi :/
Damian: |2x+2| + |x−1| = x+ 3
w rozwiązaniu sa 3 przedziały
(−
∞,−1) ; <−1,1> ; (1, +
∞)
dla pierwszego będzie x =−1 x nie nalzy do przedziału
dla drugiego bedzie 3=3 wiec cały przedział
dla trzeciego x=1 nie należy...
SKĄD MAM WIEDZIEĆ JAK POWIĄZAĆ PRZEDZIAŁY

? bo ja zrobiłem takie:
(−
∞,−1) ; <−1,1) ; <1, +
∞)
jak i kiedy mam je domykać

? bo rozwiązanie się zmieni

26 kwi 23:19
Damian: 
26 kwi 23:26
Jack: po pierwsze, rozpisz porządnie moduły. Zobaczysz że wyjdą Ci trzy przedziały. Dla każdego z
nich szukaj rozwiązania. Z definicji modułu masz zapisane kiedy "domykasz", a kiedy nie.
26 kwi 23:36
Damian: wiem zeby szukać rozwiązan dla przedziałów − ale kiedy je domykać

?
26 kwi 23:44
Jack:
np jak rozpiszesz pierwszy moduł masz:
2(x+1) dla x≥−1 (1)
2|x+1|= 2(−x−1) dla x<−1 (2)
Drugi:
(x−1) dla x≥1 (3)
|x−1|= (−x+1) dla x<1 (4)
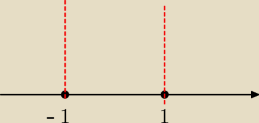
Stąd masz dwie liczby które dzielą CI oś OX: −1 i 1.
Widac z rys. ze masz trzy przedziały. Pierwszy to będzie (−∞,−1
). Teraz pytanie o to czy
")" czy ">" W tym celu patrzymy na moduł. Warunek (2) który określa ten przedział daje nam
ostrą nierówność.
Gdy weźmiemy przedział drugi z rys (pomiędzy −1 a 1) to znów patrzymy na def. Widzimy że
warunek (1) mówi o punktach x
≥−1 z kolei (4) o punktach x<1 (nie ma w żadnej definicji
np. przedziału x
≤1) więc mamy x∊<−1,1) itd
26 kwi 23:55
 ? bo ja zrobiłem takie:
(−∞,−1) ; <−1,1) ; <1, +∞)
jak i kiedy mam je domykać
? bo ja zrobiłem takie:
(−∞,−1) ; <−1,1) ; <1, +∞)
jak i kiedy mam je domykać  ? bo rozwiązanie się zmieni
? bo rozwiązanie się zmieni 

 ?
?
 np jak rozpiszesz pierwszy moduł masz:
2(x+1) dla x≥−1 (1)
2|x+1|= 2(−x−1) dla x<−1 (2)
Drugi:
(x−1) dla x≥1 (3)
|x−1|= (−x+1) dla x<1 (4)
Stąd masz dwie liczby które dzielą CI oś OX: −1 i 1.
Widac z rys. ze masz trzy przedziały. Pierwszy to będzie (−∞,−1). Teraz pytanie o to czy
")" czy ">" W tym celu patrzymy na moduł. Warunek (2) który określa ten przedział daje nam
ostrą nierówność.
Gdy weźmiemy przedział drugi z rys (pomiędzy −1 a 1) to znów patrzymy na def. Widzimy że
warunek (1) mówi o punktach x≥−1 z kolei (4) o punktach x<1 (nie ma w żadnej definicji
np. przedziału x≤1) więc mamy x∊<−1,1) itd
np jak rozpiszesz pierwszy moduł masz:
2(x+1) dla x≥−1 (1)
2|x+1|= 2(−x−1) dla x<−1 (2)
Drugi:
(x−1) dla x≥1 (3)
|x−1|= (−x+1) dla x<1 (4)
Stąd masz dwie liczby które dzielą CI oś OX: −1 i 1.
Widac z rys. ze masz trzy przedziały. Pierwszy to będzie (−∞,−1). Teraz pytanie o to czy
")" czy ">" W tym celu patrzymy na moduł. Warunek (2) który określa ten przedział daje nam
ostrą nierówność.
Gdy weźmiemy przedział drugi z rys (pomiędzy −1 a 1) to znów patrzymy na def. Widzimy że
warunek (1) mówi o punktach x≥−1 z kolei (4) o punktach x<1 (nie ma w żadnej definicji
np. przedziału x≤1) więc mamy x∊<−1,1) itd