Oblicz: stachu: pole figury opisanej układem nierówności: (x−5)²+(y−2)²≤20 x−2y+4≤0

Basia: jaka to szkoła ? średnia czy studia ? pytam, bo nie wiem czego mogę używać

stachu: średnia, ale całki jak najbardziej wskazane

Basia: tak czy owak jest to wredne spróbuję to policzyć, ale za jakąś godzinkę, bo muszę teraz skoczyć do sklepu po paliwo napędowe i jakąś kolację zjeść

stachu: aby pomóc powiem od razu, że prosta ta ogranicza fragment okręgu w połowie promienia, w pewnym momencie się zacinam

Basia: A,B p−ty wspólne SA=SB=r SD wysokość ASB prostopadła do AB jeżeli SD=^r₂ ( a jest bo to odległość S od prostej) to dalej jest łatwo AD²+SD²=AS²

	r2		3r2
AD2=r2−		=
	4		4

	r√3
AD=
	2

	AD		√3
sin∡ASD=		=
	AS		2

∡ASD=60 ⇒ ∡ASB=120 wycinek ASB ma pole = ¹₃πr²

	r√3		r
Ptr.ASB=		*
	2		2

P_szukane=P_wycinka−P_trójkąta

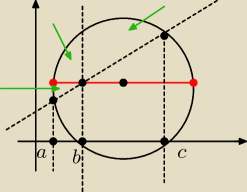
Jack: weź y=√(x−5)²+20+2 dla koła nad czerwoną linią i y=−√(x−5)²+20+2 dla koła pod czerowną linią. Musisz policzyć pole tych trzech kawałków wskazanych zieloną strzałką (o ile niczego nie pomyliłem). Kilka punktów trzeba wyznaczyć ale to już chyba mały problem.

Basia: Witaj Jack. Moje rozwiązanie prościutkie. Cała sztuka zauważyć, że odległość środka od prostej = ^r₂, ale to już stachu zauważył.

Jack: Tak tak, rzeczywiście prościej − po prostu padła sugestia użycia całki więc nie myśląc już (o tej porze) wiele, podałem przepis Twoje rozwiązanie jest zdecydowanie lepsze!

stachu: Właściwie to chciałem zobaczyć obydwa rozwiązania, ale skoro bez użycia całki jest o tyle prościej to już nie będę wam zawracał gitary, dzięki