Nierówność Kisiel: Dana jest nierówność |x − 1| + |x + 2| < m. Wyznacz te wartości parametru m, dla których ta nierówność nie ma rozwiązań.

stachu: rozpatrujesz 3 przypadki kiedy: I. x<−2 II. −2≤x<1 III. x≥1 1. −x+1−x−2=0 −2x−1=0 2. −x−1+x+2=0 brak rozwiązań 3. x−1+x+2=0 2x+1=0 nierówność nie ma rozwiązań dla m<3

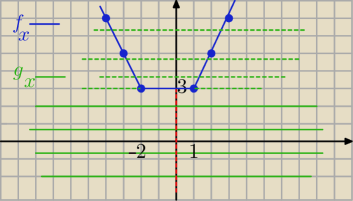
Eta: Najprościej rozwiązać rysyjąc wykresy: f(x) = I x−1i +I x+1I i g(x)= m −−− funkcja stała rozpatrujemy f(x) w przedziałach: dla x < −2 => f(x) = −x+1 −x −2= −2x −1 dla x€<−2, 1) => f(x) = −x+1 +x +2= 3 dla x€ <1,∞) => x−1+x+2= 2x +1 rysujemy te wykresy i widać ,że dla m€ ( −∞, 3) −−− brak rozwiazań odp: m€ ( −∞, 3)