zad matthew: Wyznacz zbior wartosci funkcji f(x) = 2cos²x − cosx

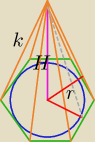
matthew: mam jeszcze takie zadanie: Oblicz objetosc ostroslupa prawidlowego szesciokatnego wiedzac, ze dlugosc krawedzi bocznej wynosi k oraz promien okregu wpisanego w podstawe tego ostroslupa wynosi r. prosze o pomoc

matthew: wiedzialbym jak rozwiazac zadanie, gdybym mial okrag opisany, natomiast ze wpisanym mam problem.... prosze o jakas podpowiedz

Eta: r= h( trójkąta równoboczneg) o boku dł; "a"

	a√3
r=
	2

	2√3 r
to a=
	3

	a2√3
Pp= 6*		=.....
	4

H ostr. wyznacz z tw. Pitagorasa z trójkąta prostokatnego H, a, −−− dł. przyprostokątnych , k −−dł. przeciwprostokątnej

Godzio:

	a√3
r =
	2

	2r
a =
	√3

1
	a2 + h2 = k2
4

1		4r2
	*		+ h2 = k2
4		3

r² + 3h² = 3k² 3h² = 3k² − r²

	3k2 − r2
h2 =
	3

H² + r² = h²

	3k2 − r2		3r2
H2 =		−		= {3k2 − 4r2}{3}
	3		3

	√3k2−4r2
H =
	√3

	a2√3		4r2   3 * * √3   3
Pp = 6 *		=		= 2√3r2
	4		2

	1		1		√3k2−4r2		2r2√3k2−4r2
V =		* Pp * H =		* 2√3r2 *		=
	3		3		√3		3

sprawdź czy nigdzie się nie pomyliłem

tylkoniematma: na to pierwsze f(x)=2cos²(x)−cos(x) czyli 2cos²(x) − cosx= 0 cos(x)(2cos(x)−1)=0 dla cosx=o dla x={π/2 +kπ} dla cosx=1/2 dla x={π/4 +kπ} gdzie k ∊ C

matthew: ok. wyszlo dzieki Eta

matthew: Oblicz wartoc wyrazenia:

(x−y)(x4−y4)		2xy(x3 − y3)
	−
x2 − y2		x2 + xy + y2

zaczalem tak:

(x−y)(x4−y4)		2xy(x3 − y3)
	−		=
x2 − y2		x2 + xy + y2

	(x−y)(x2 − y2)(x2+y2)		2xy(x−y)(x2 + xy + y2)
=		−		=
	(x−y)(x+y)		x2 + xy + y2

	(x−y)(x+y)(x+y)2 − 2xy
=		− 2xy(x−y) = (x−y)(x+y)2 − 2xy − 2xy(x−y)
	x+y

Godzio: 2 linijka

(x−y)(x−y)(x+y)(x2+y2)		2xy(x−y)(x2+xy+y2
	−		=
(x−y)(x+y)		x2+xy+y2

(x−y)(x²+y²) − 2xy(x−y) = (x−y)(x² + y² − 2xy) = (x−y)(x−y)² = (x−y)³

matthew: sorki, przyakdkiem wyslalem... to jest dokonczenie: = (x−y)(x² + 2xy + y²) − 2xy − 2xy(x−y) = x²(x−y) + 2xy(x−y) + y²(x−y) − 2xy − 2xy(x−y) = = x²(x−y) + y²(x−y) − 2xy .... nie wiem co zrobic dalej...

	7
mam jeszcze takie dane: x = 1,(2) i y = 2
	9

musze je wstawic do tego wyrazenia powyzej, ale wychodza mi zle wyniki.... nie wiem wlasciwie jak interpretowac ta liczbe x = 1,(2).... prosze o pomoc

Godzio:

	11
x = 1,(2) =
	9

	7		25
y = 2		=
	9		9

podstaw a dalej sobie już dasz radę

matthew: dzieki Godzio wyszlo a mozesz napisac mi jak przeksztalciles liczbe 1,(2) do postaci ulamkowej?

Eta: 1, (2) = x /*10 12, (2) = 10x odejmujemy:

	11
11= 9x => x=		= 1 29
	9

Godzio:

matthew: mam jeszcze takie zadanie....

	1
Dana jest funkcja f(x) =		. Wyznacz rownanie prostej y = ax + b (a≠0), ktora z wykresem
	2

	1
funkcji ma tylko jeden punkt wspolny A(2,		)
	2

podstawilem ten punkt do prostej, tak jak zwykle nalezy zrobic kiedy wyznaczamy wzor f. liniowej. brakuje jeszcze jednego punktu.... myslalem, ze to jeden z nich (0, y) lub (x,0) − zdawajac sobie sprawe, ze bede musial sie jeszcze uporac z x i y − poniewaz prosta przecina oby dwie osie.... jendak nie wiele to pomoglo.... prosze o jakas podpowiedz

matthew: o dziekuje wam

Godzio: Coś za mało danych żeby podać dokładne równanie tej prostej

matthew: ... nie rozumiem za bardzo.... szczerze pierwszy raz spotykam sie z czyms takim jak 1,(2) co to w ogole jest za liczba? nie za bardzo rozumiem to odejmowanie... tzn co od czego dokladnie jest odejmowane....? i dlaczego nalezy mnozyc razy 10?

matthew: ja tam sie pomylilem.... dopiero teraz zauwazylem....sorki... wzor funkci ma wygladac tak:

	1
f(x) =		parabola
	x

Godzio: mnożysz zawsze tyle 10 ile jest liczb w okresie np. 1.(123) = x tutaj razy 1000 1,(23) = x / * 100 itd 1,22222 = x / * 10 12,2222 = 10x / − x 12,2222 − x = 9x 12,2222 − 1,2222 = 9 x 11 = 9x

	11
x =
	9

Teraz zrozumiałe ?

Godzio: jak coś to hiperbola dobra to robimy

matthew: no wlasnie

matthew: ale ja tylko o podpowiedz prosze, bo chcialbym sam zrobic to zadanie

stachu: jak masz tylko jeden punkt to przechodzi przez niego pęk prostych ograniczony ramionami hiperboli

Godzio:

	1
f(x) =
	x

	1
A(2,		)
	2

y = ax + b a ≠0

1
	= 2a + b
2

	1
b =		− 2a
	2

	1
y = ax +		− 2a
	2

f(x) = y

1		1
	= ax +		− 2a / * x
x		2

	1
ax2 (		− 2a)x − 1 = 0
	2

zał. Δ = 0

	1		1		1
Δ =		− 2a + 4a2 + 4a = 4a2 + 2a +		= (2a +		)2 = 0
	4		4		2

	1
(2a +		)2 = 0
	2

	1
a = −
	4

	1		1		1		1
y = −		x +		+		= −		x + 1
	4		2		2		4

Godzio: AA to nie patrz na to Podstaw punkt A do prostej oblicz "a" lub "b" Przyrównaj y do f(x) i że ma być tylko jeden punkt wspólny Δ = 0

stachu: i tak na prawde rozwiązaniem będzie prosta x=2, ponieważ inaczej prędzej czy później jakakolwiek prosta przetnie hiperbole ponieważ one dążą do obu nieskończoności

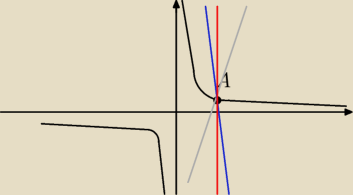
stachu: A Poprowadźmy jakąkolwiek prostą z współczynnikiem kierunkowym dodatnim (szara) i ujemnym (niebieska). Prędzej czy później nastąpi drugie przecięcie. Jedynym rozwiązaniem jest x=2 (czerwona)

Godzio: ano też prawda

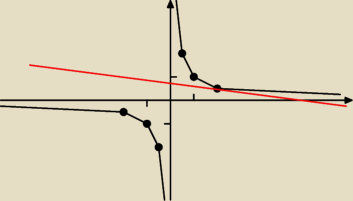
Godzio: a taka ?

stachu: pisałem już wcześniej, że to będzie pęk prostych ograniczony hiperbolami, takich prostych będzie dużo

stachu: znaczy przepraszam, będzie styczna do tego punktu i x=2, przepraszam najmocniej

matthew: ale spojrzcie na tresc zadania jeszcze raz jest tam maly szczegol, ktory rozwiewa wszelkie watpliwosci dziekuje wam za odpowiedzi

matthew:

	1
a jednak nie, pomylka, sorki, chodzilo mi o ten warunek a≠0, ale to tyczy sie tylko y =
	2

tzn ze x = 2 rowniez jest dobry, wiec mam brac pod uwage dwie odpowiedzi?

stachu: skoro nic nie ogranicza to rozwiązaniami są styczna do hiperboli w I ćwiartce układu w punkcie P i x=2

matthew: Godzio z tym okresem jest prawie wszystko zrozumiale, tylko dlaczego akurat po przecinku

	1
jest 5 dwojek? czy to wynika z tego, ze 0,2 to		?
	5

i na koncu jak podstawiasz za x liczbe, dlaczego ona ma po przecinku cztery cyfry, skoro na poczatku x byl rowny: 1,22222 ? dlaczego nalezy odejmowac x po obu stronach?

stachu: czy to 5 dwójek czy to 1289, nie ważne. Właśnie po to jest okres to jest liczba 2 po przecinku dążąca do nieskończoności. A jak odejmujesz stronami to okres też odejmujesz. Stąd z 12,(2) − 1,(2) = 11.

matthew: W trojkacie o bokach dlugosci 5, 7, i 8 oblicz dlugosc srodkowej poprowadzonej do najdluzszego boku. Prosze o pomoc

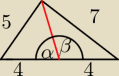
stachu: β=π−α cosβ=−cosα I użyj 2x twierdzenia kosinusów.

asda: ΔΩ⇒αβδπ∄Ωβ⇒ΩΔ∑≈⇒∫→ i wtedy wam wyjdzie

asda: 75 11² 112 x³ + x² + x + 1 x3 + x2 + x + 1 5¹⁰ 510 8^2x−1 + 4^x = 2 82x−1 + 4x = 2 2²⁰⁰⁹ 22009 64 = 8² = (2³)² = 2^3*2 = 2⁶ 64 = 82 = (23)2 = 23*2 = 26 3⁴⁵ 345 5^x2−2 5x2−2 x^x2 = e^{ln xx2} = e^x2lnx xx2 = eln xx2 = ex2lnx √3 √3 √121 √121 ³√8 3√8 ⁴√625 4√625 3 ^√2 3 √2 ²₃ 23 1⁴₅ 145 ²₇ + ³₇ = ⁵₇ 27 + 37 = 57 (1²₃ − 2⁷₈) * ⁴₅ (123 − 278) * 45

1		2		4
	+		− 1
2		3		5

1 2 4 + − 1 2 3 5

3x − 2
2x + 1

3x − 2 2x + 1

2 + 12
13 − 45

2 + 12 13 − 45

3 + 14   2 +   7 − 89
5

3 + 14 2 + 7 − 89