Daroos: cosx-cos3x=sinx-sin3x Możecie mi pomóc z tym zdaniem? Bardzo Was prosze...

Dariusz: cosx - 4cos³ x + 3 cosx = sinx - 3sinx + 4sin³ x 4cosx - 4cos³ x = -2sinx + 4sin³ x 2cosx - 2cos³ x = 2sin³ x - sinx 2cosx(1-cos² x)= 2sin³ x - sinx 2cosx(sin² x) = 2sin³ x - sinx 2cosxsin²x = 2sin³ x - sinx Zalozenie: sinx ≠ 0 2cosxsinx = 2sin² x - 1 2cosxsinx = sin² x + 1 - cos²x - 1 2cosxsinx = sin² x - cos²x 2cosxsinx = 1 - cos²x - cos²x 2cosxsinx + 2cos²x = 1 cosxsinx + cos²x = 1/2 cosx(sinx+cosx)=1/2 Powiem Ci szczerze, nie znam sie na tym ale mozna by sprobowac zauwazyc, ze wykres funkcji cosx jest przesunietym wykresem sinx o pewien wektor i jakos to podstawic, ale jak juz powiedzialem nie znam sie; Dla sinx=0 latwo wszystko zrobic

Domi: (1+sinα)(1−sinα)+sin2

Bogdan: cosx − cos3x = sinx − sin3x Korzystamy z:

	α+β		β−α		α−β		α+β
cosα − cosβ = 2sin		sin		oraz sinα − sinβ = 2sin		cos
	2		2		2		2

2sin2x sinx = 2sin(−x) cos2x ⇒ 2sin2x sinx + 2sinx cos2x = 0 ⇒ 2sinx(sin2x + cos2x) = 0 sinx = 0 ⇒ x = k*π lub

	π
sin2x = −cos2x ⇒ cos(		− 2x) = cos(π − 2x)
	2

π
	− 2x = π − 2x + k*2π sprzeczność
2

lub

π		3		3		π
	− 2x = −π + 2x + k*2π ⇒ 4x =		π − k*2π ⇒ x =		π − k*
2		2		8		2

	3		π
Odp.: x = k*π lub		π − k*
	8		2

PW: Bogdanie, coś chyba nie tak. Równość sin2x = −cos2x ma pierwiastki. Nie wdając się w dyskusję kiedy można podzielić, podzielmy:

	sin2x
		= −1
	cos2x

tg2x = −1 ma pierwiastki. A podzielić można, bo x, dla których cos2x=0 nie są pierwiastkami (sin2x jest dla nich różny od 0).

Bogdan: a co konkretnie nie tak? Skorzystałem z zależności:

	π
sinα = cos(		− α) oraz −cosα = cos(π − α)
	2

PW: Ale z równości typu cosβ = cosγ wyciągnąłeś wniosek, że β = γ + 2kπ, a to nie wszystkie możliwości (cosinus przyjmuje tę samą wartość na przedziale o długości 2π w dwóch punktach dziedziny z nielicznymi wyjątkami oczywiście).

Bogdan: Skorzystałem z: cosβ = cosγ ⇒ β = γ + k*2π lub β = −γ + k*2π U mnie: 2sinx(sin2x + cos2x) = 0 sinx = 0 ⇒ x = k*π lub sin2x = −cos2x

	π		π
cos(		− 2x) = cos(π − 2x), tu β =		− 2x oraz γ = π − 2x
	2		2

	π		π
β = γ + k*2π ⇒		− 2x = π − 2x + k*2π ⇒		= π + k*2π sprzeczność
	2		2

lub

	π		3
β = −γ + k*2π ⇒		− 2x = −π + 2x + k*2π ⇒ 4x =		π − k*2π
	2		2

	3		1
x =		π − k*		π
	8		2

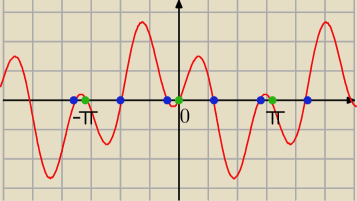
k∊C Rysunek przedstawia wykres funkcji f(x) = cosx − cos3x − sinx + sin3x. Kropki zielone i niebieskie są miejscami zerowymi tej funkcji i jednocześnie pokazują na osi rozwiązania równania cosx − cos3x = sinx − sin3x

	3		1
Odp.: x = k*π (zielone kropki) lub x =		π − k*		π (niebieskie kropki)
	8		2

Uważam, że wszystko jest dobrze. Widać na rysunku, że żadne rozwiązanie równania cosx − cos3x = sinx − sin3x nie jest pominięte (wystarczy wziąć jakieś wartości k∊C). Jeśli jednak PW podtrzymujesz swoje zdanie, że coś jest nie tak, to pokaż swoje rozwiązanie.

PW: Bogdanie, wybacz niesłuszną krytykę. Widocznie nie przewinąłem ekranu dostatecznie i nie widziałem dalszego "lub"! a od razu napisałem, że mi się nie podoba. A swoją drogą − tak dla ucznia − rozwiązanie z podzieleniem przez cos2x jest strawniejsze (tangens jest różnowartościowy na całej "podstawowej dziedzinie" i nie ma kłopotu z liczbą pierwiastków. Chyba przeciętny, nawet zdolny uczeń nie wpadnie na to

	π
cos(		−2x) = cos(π−2x).
	2

Jestem pod wrażeniem dobrej roboty (rysunek)!

Bogdan: Dziękuję PW. Pokazuję na forum różne sposoby rozwiązywania zadań, nawet takie, które są obce dla przeciętnego ucznia, po to, by taki uczeń mógł poszerzyć swoją wiedzę. Pozdrawiam.

tosia: (1+sin x)*(1/cos x −tg x =cos x