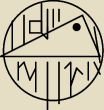
Oblicz pole majka: Oblicz pole figury zakreskowanej.

Kejt: kilka pytań.. przeciwprostokątna jest średnicą? promień masz podany?

majka: nie, wszystko na literkach ma byc

Kejt: a co z tą przeciwprostokątną?

majka: srednica jest rowna 2r a tam na gorze to jest a

majka: tak jest srednica

Jack: musi być średnicą, skoro mamy kąt prosty.

mickey: pomozecie mi?

Kejt: w sumie racja.. nie kontaktuję już chyba..

Jack: jak jeden z boków jest "a", przeciwprostokątna 2r, to policzysz z tw. Pitagorasa "b" − drugą przyprostokątną. Potem pole trojkąta to a*b/2, pole całego koła to πr². Zamalowany obszar to różnica.

Jack:

Amaz: Co tu jest dane? r tylko? czy jeszcze jakiś bok?

mickey: dzieki wielkie a dał rade bys jeszcze jedno podobne zrobić?

Jack: nie wiem, jak nie ja, to ktoś inny − wrzuć

mickey: Środki n przystających okręgów leżą na okręgu o promieniu R. Kazdy z przystających okręgów jest styczny do dwóch sasiednich okręgów. Wyznacz promień tych okręgów.

Jack: proponuje zrobić tak: Wiemy, że suma kątów wewn. wielokąta foremnego ma miarę (n−2)*180^o. Każdy kąt będzie miał

	(n−2)*180o		360o
miarę		. Kąt środkowy będzie miał miarę α=		.
	n		n

Utworzymy trójkąt równoramienny ABC o ramionach długości R i wierzchołkach w środkach dwóch okręgów przystających (A i B) oraz środka dużego okręgu O. Zauważymy że punkt styczności leży zawsze w połowie boku AB. Zatem szukanym promieniem jest połowa tego odcinka. Odcinek łączący środki wierzchołków (czyli AB) okręgów przystających wyliczymy ze wzoru

	|AB|
sin(α2)=1/2|AB|R ⇔		=sin(α/2)*R.
	2

majka : Dzięki wielkie jestem naprawde wdzięczna Jack

Jack: proszę bardzo