stożek chinka365: Trójkąt prostokątny o bokach dl.: 2√6, 4√3 i 6√2 obraca się dokoła przeciwprostokątnej. Oblicz: a)objętość powstałej bryły b) pole powierzchni tej bryły i jeśli mogę prosić to rysunek

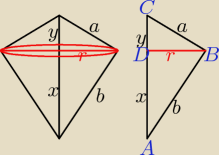
Basia: To są dwa ostrosłupy. Promień podstawy w obu = r Wysokość pierwszego = y; drugiego x 2√6=√4*6=√24 4√3=√16*3=√48 6√2=√36*2=√72 czyli 2√6<4√3<6√2 ⇒ a=2√6 b=4√3 c=6√2 x+y=c x+y=6√2 tr.BDC ~ tr.ABC ^r_b=^a_c=^y_a r=^a*b_c

	2√6*4√3		8√18		8
r=		=		=		*√182 = 43*√9=43*3=4
	6√2		6√2		6

	a2
y=
	c

	4*6		4√2
y=		= U{4}{√2=		=2√2
	6√2		2

x=6√2−y=4√2 V=V₁+V₂ P=P_b1+P_b2 podstaw do wzorów i wykonaj obliczenia

chinka365: nie wychodzi mi jeszcze prawidłowy wynik pola całkowitego, ponieważ wynik ma wyjść 8(√6+2√3)π