pomocy hiii: W trójkącie ABC: A(6, −1), B(−2,−3), C(4,−5) a) wyznacz równanie prostej zawierającej wysokość hB b) oblicz odległość punktu B od prostej AC

aaaaa: W trójkącie ABC: A(6, −1), B(−2,−3), C(4,−5) a) wyznacz równanie prostej zawierającej wysokość hB b) oblicz odległość punktu B od prostej AC

matthew: liczymy srodek prostej AC: a) A(6, −1), B(−2,−3), C(4,−5) A(x_A, y_A)

	xA+xC		yA + yC
S = (		;		)
	2		2

	6+4		−1 − 5
S = (		;		) = (5; −3)
	2		2

h = (5; −3) wzor f. liniowej: y = ax+b tworzymy uklad rownan: podstawiam punkty B i h do wzoru: {−3 = 5a + b − {−3 = − 2a + b −−−−−−−−−−− 0 = 7a a = 0 b = −3 prosta przechodzaca przez punkty h i B, to: y = −3 b) obliczam prosta AC wykorzystuje ten sam wzor, czyli y = ax + b podstawiam wspolrzedne punktow A i C: {−1 = 6a + b − {−5 = 4a + b −−−−−−−−−−−− 4 = 2a a = 2 −1 = 12 + b b = −13 prosta AC: y = 2x − 13 aby obliczy odleglosc punktu od prostej nalezy

	|A*x0 + B*y0 + C|
skorzystac z tego wzoru: d =
	√A2 + B2

gdzie punkt np. P = (x₀; y₀) w zadaniu to bedzie punkt B prosta AC : y = 2x − 13 przeksztalcamy do takiej postaci: −2x + y +13 = 0 A B C i liczymy:

	|−2 * (−2) + 1 * (−3) + 13|		|4 − 3 + 13|		14
d =		=		=		=
	√(−2)2 +12		√4+1		√5

	14		√5		14√5
=		*		=
	√5		√5		5

	14√5
odleglosc punktu B od prostej, to:
	5

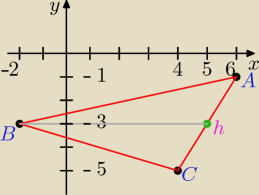
matthew: tak wyglada to na ukladzie

aaaaa: dzieki

walet: A co za głupoty podał matthew?

matthew: racja, w punkcie pierwszym nalezy wyprowadzic wzor na prosta prostopadla do prostej AC skoro mamy juz wzor prostej AC, czyli y = 2x − 13 to mozemy obliczyc prosta prostopadla i to ona bedzie wysokoscia. taki jest wzor na prosta prostopadla: a₁ * a₂ = −1 a − wspolczynnik, w naszym wypadku jest to 2, wiec a₁ = 2 2*a₂ = − 1

	1
a2 = −
	2

	1
wzor przyjmuje postac y = −		x + b
	2

prosta ma przechodzic przez punkt B, wiec wspolrzedne tego punktu wstawiam do wzoru:

	1
−3 = −		* (−2) + b
	2

b = − 4

	1
odp. : y = −		x − 4
	2

sorki za wprowadzenie w blad punkt b) jest dobrze

Eta: mathhew Muszę Cię zmartwić , wysokość pomyliłeś ze środkową trójkąta ! Prosta zawierająca wysokość poprowadzona z punktu B to prosta prostopadła do AC ( widać to na Twoim rys. ,że hB nie jest wysokością współczynnik kierunkowy prostej AC : a_AC= 2 to wsp. kier. prostej h_B : a_hB= −¹₂ zatem ma równanie hB: y = −¹₂( x − x_B) +y_B Reszta ok

matthew: Eta musze Cie zmartwic, niestety sie zrehabilitowalem

Eta: Dopiero . po uwadze waleta

matthew: jeszcze raz sorki, za wprowadzanie w blad...ech

matthew: dzieki walet jestem Ci winien zimne.... zimna cocacole

Eta: