Zbadaj liczbę rozwiązań równania A.! :) : Korzystając z wykresów odpowiednich funkcji zbadaj liczbę rozwiązań równania w zależności od wartości parametru m, gdzie m∊R a) |−x² + 1| = m b) ||x−1| − 2| = − 3m

A.! :) : bardzo proszę o pomoc chodzi mi dokładniej o to, jak rozpisać te funkcje stopniowo... i narysować każdą z nich na wykresie...

A.! :) : czy ktoś jest w stanie to zrobić?

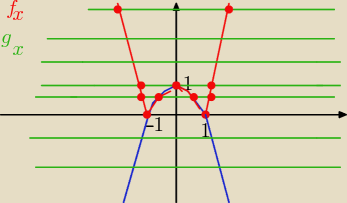
Eta: h(x) = −x²+1 −−− wykres niebieski ( parabola ) f(x) = I −x²+1 I −−− wykres czerwony ( bo odbicie tej części niebieskiego z pod osi nad oś oX g(x) = m −−− funkcja stała −−− wykres zielony teraz patrzymy , ile razy wykres zielony przecina wykres czerwony: zatem równanie I −x²+1I = m ma: dla m€( −∞, 0) −−− brak rozwiązań ( bo te wykresy się nie przecinają) dla m= 0 lub m€(1, +∞) −− dwa rozwiązania ( bo przecinają się w dwu punktach dla m= 1 −−− trzy rozwiązania dla m€( 0,1) −−− cztery rozwiązania

A.! :) : dzięki wielkie teraz wydaje się to dużo łatwiejsze.! dziękuję

A.! :) : dzięki wielkie teraz wydaje się to dużo łatwiejsze.! dziękuję

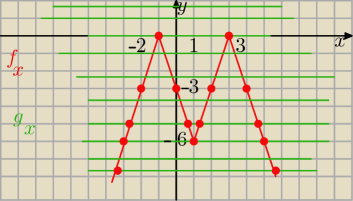
Eta: | I x −1| −2|= −3m /*(−3) f(x) = −3 ||x−1|−2| −−−−−−− zrób tabelkę i podaj kilka punktów otrzymasz czerwony wykres g(x) = m −−− funkcja stała −−− zielone wykresy odczytaj teraz podobnie jak w poprzednim zadaniu ilość punktów wspólnych wykresów czerwonego z zielonym i podaj przedziały dla "m" myślę ,że teraz już sbie poradzisz sama

A.! :) : tak tak, odczytywać umiem problem mam jedynie z wyprowadzeniem tej funkcji z podstawowej ok ok super, jeszcze raz dzięki