pomocy kaśka: Może ma ktoś jakiś pomysł jak rozwiązać to zadanie Pomóżcie Podstawą ostrosłupa ABCS jest trójkąt równoboczny ABC o boku długości 8. Punkt D jest środkiem krawędzi AB , odcinek DS jest wysokością ostrosłupa. Krawędzie AS i BS mają długość 7. Oblicz długość krawędzi CS tego ostrosłupa. Odp.CS=9

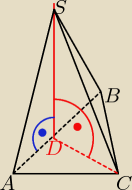Basia: CD jest środkową ABC (jest też jego wysokością, bo to tr.równoboczny)

	8√3
|CD|=		= 4√3
	2

	|AB|
|AD|=		=4
	2

|AS|=7 SD jest środkową tr.równoramiennego ASB, jest więc również jego wysokością |SD| oblicz z tw.Piragorasa w tr.ADS mając |SD| z tr.CDS i tw.Pitagorasa o blicz |CS|

robinka: |CS|²=|DS|²+ |DC|²

	a*√3
h=|DC|=		> wzór na wysokość w trójkacie równobocznym
	2

	8*√3
h=		=4√3
	2

z twierzenia pitagorasa obliczamy |DS] =x 7²= 4² +x² 49=16 +x² x²=33 x=√33 obliczamy z twierzenia pitagorasa obliczamy |CS]=y y²=x²+h² y²=33+48=81 y=9