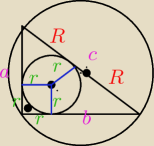
help! Wydi: Proszę o spr mojego zadania. Oblicz stosunek promienia okręgu opisanego na trójkącie prostokątnym(R) do promienia wpisanego w okrąg wewnątrz trójkąta(r) .

1		a+b+c
	ab=P=pr gdzie p=
2		2

a+b+c		ab
	*r=
2		2

r(a+b+c)=ab

	ab
r=
	a+b+c

	c		R		c		a+b+c		c(a+b+c)
R=		→ stosunek		=		*		=
	2		r		2		ab		2ab

Dobrze jest? Jeśli nie proszę o wskazówki...

Jack: Można z tego: r=^a+b−c₂ R=^c₂ ^R_r=^c_a+b−c Przyjrzę się temu co napisałeś...

Jack: jest ok

Wydi:

	a+b−c
ale jak r=		?
	2

Jack: hmm... Może opisowo spróbuję. Zauważ, że środek okręgu wpisanego wyznaczają dwusieczne kątów (np. dwóch kątów ostrych). Tworzą one przystające trójkąty (od wierzchołka przez środek okręgu do boku trókąta). Cały odcinek "a" można podzielić na r+(a−r), z kolei odcinek "b" na r+(b−r). Z tego, że masz przystające trójkąty wyniknie (po narysowaniu trójkąta), że "c" jest sumą (a−r)+(b−r). To oznacza, że c=a−r+b−r ⇒ 2r=a+b−c ⇒ r=^a+b−c₂

Eta: c= a−r +b−r => c= a+b −2r => 2r= a+b −c to:

	a+b−c
r=
	2

Wydi: O dziękuję za wizualizacje już zdążyłem zrozumieć ale rysunek rozwiał wszelkie wątpliwości

Eta:

Jack: