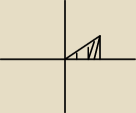
prosze o pomoc paweł: ∫∫xydxdy A=(0,0) B=(2,0) C=(2,1)

robinka: ja bym to zrobiła tą całkę tak w granicach od 0 do 2> ∫2xdx = [2*¹₂x²]²₀ = 4−0=4

Basia: tu nie chodzi, jeśli dobrze rozumiem, o pole to jest całka podwójna funkcji dwóch zmiennych f(x,y)=x*y po obszarze △ABC dobrze rozumiem ?

paweł: a jakoś bardziej łopatologicznie bo to dla mnie czarna magia ...

Basia: napisz najpierw czy dobrze rozumiem treść zadania chodzi o całkę podwójną ?

paweł: tzn był brak polecenia i z tegoi co doszedłem trzeba policzyć całke z ∫₀²∫₀^0,5x xydxdy

robinka: podobnie jak ja zrobiłam zadanie tylko sie pomyliłam bo powinno być granice od 0 do 2 ∫¹₂xdx > zapisałam to przy pomocy całki pojedynczej. [¹₂ *¹₂ x²]₀²= ¹₄*4−0=1

Basia: prawie ∫₀² [ ∫₀^0,5x xy dy ]dx ale zastanawiam się czy to nie jest ¹₂ całki po prostokącie [0,2]x[0,1] i zdaje mi się, że jest, bo w trójkącie ADC gdzie D(0,1) dla P(x₀,y₀)∊ACD R(y₀,x₀)∊ABC i to jest przyporządkowanie wzajemnie jednoznaczne F(x₀,y₀)=x₀*y₀ = y₀*x₀ na a całka po prostokącie to Pikuś (no pan Pikuś) ∫₀¹[ ∫₀² xy dx ] dy = ∫ [ ¹₂x²y |{0≤x≤2| ] dy = ∫₀¹ 2y dy = y² |₀¹ = 1−0=1 Twoja całka = ¹₂ ale głowy za to nie dam

Basia: robinko to co liczysz to całka po prostokącie

paweł: oki dziekuje slicznie za pomoc

paweł: Basiu sprawdzisz moj tok rozumowania ewentualnie ktoś kto sie na tym zna ∫₀²[ ∫₀^0,5x xydy]dx= ∫₀²[^xy2₂]₀^0,5x dx = ¹₂∫₀²[xy²]₀^0,5x = ¹₂∫₀² x*^x2₄ dx = ¹₂∫₀^{2 x3}₄dx= ¹₈[x³dx]₀² = ¹₈* [^x4₄]₀²= ¹₈* ¹⁶₄= ¹₂

Basia: dobrze jest w drugim od końca znaku całki brakuje (ale to tylko chochlik w zapisie) =¹₈∫_{0 do 2} x³ dx = ¹₈*^x4₄ |₀² = ¹₃₂*[ x⁴ ]₀² = ¹₃₂*[ 2⁴−0⁴] = ¹₃₂*16=¹₂

paweł: dziekuje ślicznie mam pytanko czy podała być swojego email jeśli być mogła bym był wdzieczny niesamowicie