5.Dany jest wielomian W(x)=x3+ax2-bx-6 Liczby 1 i 2 są pierwiastkami tego wie krystian prosi o pomoc: 5.Dany jest wielomian W(x)=x3+ax2−bx−6 Liczby 1 i 2 są pierwiastkami tego wielomianu. 1. wyznacz współczynnik a i b 2. Przy wyznaczonych a i b rozwiąż nierówność W( x)>0

Basia: W(1)=W(2)=0 W(1)=1³+a*1²−b*1−6 = 1+a−b−6 = a−b−5 stąd a−b−5=0 a−b=5 −−−−−−−−−−−− W(2)=2³+a*2²−b*2−6=8+4a−2b−6=4a−2b+2 stąd 4a−2b+2=0 4a−2b=−2 /:2 2a−b=−1 −−−−−−−−−−−−−−−− rozwiąż układ podkreślonych równań wyznacz a,b podstaw za a,b do wzoru wielomianu podziel W(x) przez (x−1)(x−2) = x²−3x+2 dostaniesz jakiś dwumian x+c W(x)=(x−1)(x−2)(x+c) rozwiązujesz nierówność (x−1)(x−2)(x+c)>0

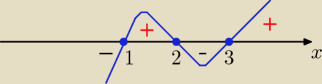
Eta: W(1)=0 i W(2)=0 W(1)= 1+a−b−6= a−b−5 to a−b−5=0 W(2)= 8+4a−2b−6=4a−2b+2 to 4a−2b+2=0 / : (−2) a−b=5 −2a+b= 1 −−−−−−−−− −a= 6 => a= −6 to b= −11 dzielimy W(x) przez (x−1)(x−2) = x²−3x +2) ( x³ −6x² +11x −6 : ( x²−3x+2)= x −3 −x³ +3x² −2x −−−−−−−−−−−−−− = −3x² +9x −6 3x² −9x +6 −−−−−−−−−−−−−−− = = = W( x) = ( x−1)(x−2)(x−3) >0 to: x€ (1,2) U ( 3,∞)

Gustlik: Eta, nie prościej schematem Hornera zamiast dzielić słupkiem? Wiesz, że 1 i 2 są pierwiastkami. Liczę W(1) i dzielę jednocześnie przez (x−1): W(x) 1 −6 11 −6 ← współczynniki W(x) 1 1 −5 6 0 ← reszta = W(1)=0 Tak to się oblicza: Pierwszy współczynnik wyniku dzielenia, czyli 1 musi byc równy pierwszemu wspólczynnikowi wielomianu W(x), czyli 1, a więc go spisujesz do drugiego wiersza. Dalej robisz tak: 1*1+(−6)=−5 1*(−5)+11=6 1*6+(−6)=0 Otrzymujesz x²−5x+6 (liczby zaznaczone na czerwono to współczynniki wyniku dzielenia − jest to wielomian stopnia o 1 mniejszego niz poprzedni, a więc w tym przypadku funkcja kwadratowa). Δ=b²−4ac=(−5)²−4*1*6=25−24=1 √Δ=1

	−b−√Δ		5−1
x1=		=		=2 ← to drugi pierwiastek podany w treści zadania
	2a		2

	−b+√Δ		5+1
x2=		=		=3 ← to trzeci pierwiastek.
	2a		2

Dalej − jak narysowałaś. Pozdrawiam.

xdu: 5x3−20x

6-latek: 5x(x−2)(x+2)