

 no dobra jakoś poszło ale jak masz jakieś odpowiedzi czy cos to fajnie bylo by to sprawdzić bo
nie lubie planimetri. A policzyłem to tak a że jest ownoramieny to wywnioskowalem, że kąty β
są oparte na tym samym łuku, wiec maja takie same miary. A kąty policzylem tak te wysokości sa
prostopadłe wiec α+90+90+2α2=360
z tego wyszlo 60 stopni. A że wiemy sie jest równoramiany no to 2β+α=180 β=60 stopni ale nie
dam sobie za to glowy uciać możliwe że jest dobrze.
no dobra jakoś poszło ale jak masz jakieś odpowiedzi czy cos to fajnie bylo by to sprawdzić bo
nie lubie planimetri. A policzyłem to tak a że jest ownoramieny to wywnioskowalem, że kąty β
są oparte na tym samym łuku, wiec maja takie same miary. A kąty policzylem tak te wysokości sa
prostopadłe wiec α+90+90+2α2=360
z tego wyszlo 60 stopni. A że wiemy sie jest równoramiany no to 2β+α=180 β=60 stopni ale nie
dam sobie za to glowy uciać możliwe że jest dobrze.
 ok, te Twoje wyliczenia i wszystko tutaj rozumie. tylko nie jestem pewna do tego skad Ci sie
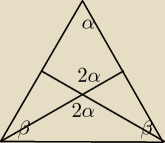
wzieło to 2α, z tego może, że kąt środkowy jest dwa razy większy od kąta wpisanego
ok, te Twoje wyliczenia i wszystko tutaj rozumie. tylko nie jestem pewna do tego skad Ci sie
wzieło to 2α, z tego może, że kąt środkowy jest dwa razy większy od kąta wpisanego
 wogole to na kartce sobie narysowalem ten trojkat i okrag na nim to wtedy wszystko
widzać idealnie.
wogole to na kartce sobie narysowalem ten trojkat i okrag na nim to wtedy wszystko
widzać idealnie.

 a jakbys jeszcze mógł napisac cos
w związku z tą pierwszą cześcią zadania to byłabym wdzięczna
a jakbys jeszcze mógł napisac cos
w związku z tą pierwszą cześcią zadania to byłabym wdzięczna
 więc dlaczego nie od razu korzystać z
tej danej przy liczeniu drugiej cześci zadania
więc dlaczego nie od razu korzystać z
tej danej przy liczeniu drugiej cześci zadania

 bo przecież jakbym wiedziasła jak to rozwiązać to bym nie
pisala tego zadania na tym forum
bo przecież jakbym wiedziasła jak to rozwiązać to bym nie
pisala tego zadania na tym forum
 ciekawe zadanie, tyle, że sama mam problem ze zrobieniem do niego rysunku
ciekawe zadanie, tyle, że sama mam problem ze zrobieniem do niego rysunku 
 cały czas coś mi tu nie gra...
szczególnie te wysokości nie mniejsze niż długości boków...
cały czas coś mi tu nie gra...
szczególnie te wysokości nie mniejsze niż długości boków...
 raz dla tedo, że ciezko mi w ogole idą
zadania w stylu "wykaz ze", "udowodnij ze", a dwa dla tego, ze nie przerobilismy planimetrii
gdyz pani zawsze zostawiala to na koniec roku i z reguly nie zdazylismy z materialem. czasami
tylko zaczelismy brac ten material ale to byla zawsze na koncu roku, a kazdy kto chodzil do
szkoly wie jak nauka na koncu roku wyglada o.O
raz dla tedo, że ciezko mi w ogole idą
zadania w stylu "wykaz ze", "udowodnij ze", a dwa dla tego, ze nie przerobilismy planimetrii
gdyz pani zawsze zostawiala to na koniec roku i z reguly nie zdazylismy z materialem. czasami
tylko zaczelismy brac ten material ale to byla zawsze na koncu roku, a kazdy kto chodzil do
szkoly wie jak nauka na koncu roku wyglada o.O 


 a molestowac nikogo nie bede bo nikogo tu
nie znam, ale dzieki
a molestowac nikogo nie bede bo nikogo tu
nie znam, ale dzieki swiat moze sie nie zawali jak tego zadania nie rozwiaze
swiat moze sie nie zawali jak tego zadania nie rozwiaze
 sama jestem ciekawa rozwiązania
sama jestem ciekawa rozwiązania 
 rysunek pomocniczy powyżej
myślę sobie tak, że jeśli wysokości trójkąta ABC mają być nie mniejsze niż długości boków do
których są prostopadłe to mogą tylko być im równe ( dłuższe raczej nie) czyli c = h2 i b =
h1.
rysunek pomocniczy powyżej
myślę sobie tak, że jeśli wysokości trójkąta ABC mają być nie mniejsze niż długości boków do
których są prostopadłe to mogą tylko być im równe ( dłuższe raczej nie) czyli c = h2 i b =
h1.
| 1 | 1 | |||
PΔABC = | b*h1 = | b*b | ||
| 2 | 2 |
| 1 | 1 | |||
PΔABC = | c*h2 = | c*c | ||
| 2 | 2 |
| 1 | 1 | |||
Stąd | b*b = | c*c i b= c czyli ΔABC jest równoramienny. | ||
| 2 | 2 |
