Problem z zadaniem dot. kąta przy okręgu Raff: W okręgu o promieniu 6 poprowadzono cięciwę AB. Długość łuku AB jest równa 2π. Oblicz miarę kąta zawartego między cięciwą AB a styczną do okręgu poprowadzoną w punkcie A.

	|β|
Tu chyba trzeba wziąć pod uwagę wzór:		2πr = l'
	360

ale co dalej?

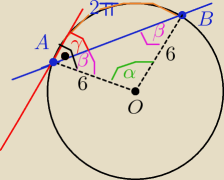
Eta: γ+β= 90^o ΔAOB jest równoramienny ( okaże się ,że jest równobocznym)

α		2π		1
	=		=
360o		2πr		6

to 6 α= 360^o => α= 60^o to

	180o−60o
β=		=> β=60o
	2

zatem : γ= 90−⁰ −β=30^o γ= 30^o

Raff: o to chodziło, dzięki

Eta: