 Cześć,
mam takie zadanie:
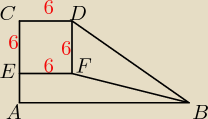
Trapez ABCD podzielono na trzy figury o równych polach. Sposób podziału ilustruje rysunek.
Wiedzac, że bok kwadratu CDEF jest równy 6, oblicz:
obwód trapezu ABCD.
zaczałem tak:
PCDEF = a2 = 36cm2
Cześć,
mam takie zadanie:
Trapez ABCD podzielono na trzy figury o równych polach. Sposób podziału ilustruje rysunek.
Wiedzac, że bok kwadratu CDEF jest równy 6, oblicz:
obwód trapezu ABCD.
zaczałem tak:
PCDEF = a2 = 36cm2
| a+b | ||
PABEF = | *h | |
| 2 |
| 6+b | ||
36 = | *h | |
| 2 |
 pomogę
pomogę

| a+6 | ||
P(ABFE) = | *h1= 36
| |
| 2 |
| a+6 | ||
więc pole trapezu ABCD : | *( 6+h1)= 108
| |
| 2 |
 biore sie za analize
biore sie za analize

 tylko.... skad od razu wiedzialas, ze nalezy stworzyc uklad tych dwoch rownan?, Tzn konkretnie
to chodzi mi o rownanie z polem calego trapezu ABCD.
To wynika z wyczucia, czy mowiac kolokwialnie
tylko.... skad od razu wiedzialas, ze nalezy stworzyc uklad tych dwoch rownan?, Tzn konkretnie
to chodzi mi o rownanie z polem calego trapezu ABCD.
To wynika z wyczucia, czy mowiac kolokwialnie  rzuca sie w oczy?
sam probowalem stworzyc taki uklad, bylem w zasadzie pewny, ze trzeba go zrobic, ale caly czas
wychodzily mi sprzeczne wyniki, albo wszystko sie redukowalo...
rzuca sie w oczy?
sam probowalem stworzyc taki uklad, bylem w zasadzie pewny, ze trzeba go zrobic, ale caly czas
wychodzily mi sprzeczne wyniki, albo wszystko sie redukowalo...
| 72 | ||
to | *( 6+h1)= 216 /*h1
| |
| h1 |
| 72 | ||
a+6= | = 24
| |
| 3 |

 ale wiesz, mozna od razu na to nie wpasc, nie sugeruja dokladnie aby skorzystac z pola calego
trapezu, jest napisane, zeby obliczyc obwod.
Zaczalem po prostu machinalnie liczyc pole kwadratu, a potem przyrownalem je do pola mniejszego
trapezu, skoro napisali, ze pola sa rowne.. Nastepnie zaczalem kombinowac z polem trojkata,
cos nie wychodzilo, wiec myslalem, ze to ja robie cos zle, albo nie znam jakiejs wlasnosci....
i tak zeszlo troche czasu. Probowalem stworzyc uklad, gdzie pole kwadratu przyrownalem do
trojkata i do mniejszego trapezu. Wlasnie z tych dwoch rownan miedzy innymi, chcialem obliczyc
wysokosc i podstawe....
ale wiesz, mozna od razu na to nie wpasc, nie sugeruja dokladnie aby skorzystac z pola calego
trapezu, jest napisane, zeby obliczyc obwod.
Zaczalem po prostu machinalnie liczyc pole kwadratu, a potem przyrownalem je do pola mniejszego
trapezu, skoro napisali, ze pola sa rowne.. Nastepnie zaczalem kombinowac z polem trojkata,
cos nie wychodzilo, wiec myslalem, ze to ja robie cos zle, albo nie znam jakiejs wlasnosci....
i tak zeszlo troche czasu. Probowalem stworzyc uklad, gdzie pole kwadratu przyrownalem do
trojkata i do mniejszego trapezu. Wlasnie z tych dwoch rownan miedzy innymi, chcialem obliczyc
wysokosc i podstawe....
 ∑∑∑βγδΔ≤⊂∫∫←→⇒
∑∑∑βγδΔ≤⊂∫∫←→⇒
 dawaj dawaj dawaj1
dawaj dawaj dawaj1 !
A TY NIE URZYWASZ MUZGU GUGALA
!
A TY NIE URZYWASZ MUZGU GUGALA