Wzór na pole czworokąta wpisanego w okrąg FusioN!: Są jakieś wzory na pole dowolnego czworokąta wpisanego w okrąg? Mam dane tylko boki.

kalafiorowa: gdy czworokat jest wpisany w okrag to suma przeciwleglych bokow jest sobie rowna natomiast gdy jest wpisany w okrat to suma przeciwleglych katow jest sobie rowna. innych wlasnosci chyba nie ma

kalafiorowa: jest jeszcze jedno kiedy czworokat jest wpisany w okrag to iloczyn dlugosci jego przekatnych jest rowny sumie iloczynow dlugosci bokow przeciwleglych

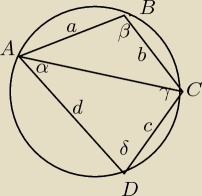AS: Jeżeli czworokąt jest wpisany w okrąg to sumy przeciwległych kątów sa równe i wynoszą 180^o. α + γ = β + δ = 180^o Można wykazać (dość łatwo) że pole czworokata wpisanego w okrąg wyraża się wzorem

	a + b + c + d
S =√(p − a)*(p − b)*(p − c)*(p − d) gdzie p =
	2

Można też liczyć:

	1		1
S =		*a*b*sin(β) +		*c*d*sin(δ) ale δ = 180 − β
	2		2

sin(δ) = sin(180^o − β) = sin(β)

	1		1
S =		*a*b*sin(β) +		*c*d*sin(β)
	2		2

	1
S =		(a*b + c*d)*sin(β)
	2