trapez... szysza1317: Może coś dla Kejt Trapez o ramionach długości 12cm i 18 cm opisany jest na okręgu o promieniu 5cm. Oblicz pole trapezu.

Panek: aby czworokat opisac na okregu sumy dlugosci jego przeciwleglych bokow musza byc rowne tzn ze suma podstaw jest rowna 30 cm wysokosc trapezu jest rona 10 cm (h=2r), teraz wystarczy pobawic sie troche pitagorasem i pomyslec.

Panek: masz do tego wynik?

Panek: Mi wyszlo 150, jesli taki jest wynik, rozwiazanie jest poprawne. Pozdrawiam

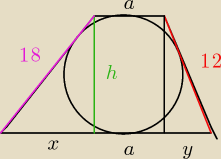
Kejt: och. dziękuję za dedykację. na rysunku widać, że wysokość tego trapezu to średnica wpisanego weń koła, więc: 2r=h h=5*2=10cm podstawy liczymy z tw pitagorasa: 18²−10²=x² x=4√14 12²−10²=y² y=2√11 chyba dobrze.. ale na "a" jeszcze pomysłu nie mam..

szysza1317: no mam wynik 150 jest hmm zaraz sama to rozkminie tym pitagorasem

szysza1317: woow ty Kejt to wymiatasz tutaj

Kejt: hah. dziękuję.

szysza1317: czy żeby obliczyć to a to trzeba : 18+12=4√14+2√11+a² i teraz nie wiem ile to a wyjdzie

Kejt: nie a² tylko 2a.. ja też nie wiem..

szysza1317: Panek ile ci wyszło to a że dobry wynik ci wyszedł z całości

Panek: wyjdzie, ze a= 15−2√14−√11, podkladasz do wzoru na pole i te liczby z pierwiastkami Ci sie uproszcza, wyglada strasznie, ale ywnik przyjemny Mam nadzieje, ze rozwiazalem problem

Kejt: dziękuję za współpracę. ;>

szysza1317: jak widzę takie liczby to aż mi się odechciewa rozkminiać to zadanie dalej heh

Panek: Pozory myla, takie zadania czesto bywaja na maturach, widzac takie liczby szukasz bledu, mimo poprawnego rozwiazania Musisz uwazac! Pozdrawiaim

mariusz: żeby obliczyć a należy skorzystać z własności czworokątów opisanych na okręgu: jeżeli w czworokąt można wpisać okrąg to sumy długości przeciwległych ramion są równe w naszym przypadku 2a+x+y=30