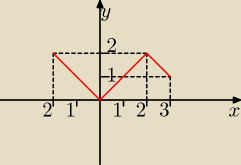
Podany wykres funkcji f(x) przekształć aby uzyskać funkcję Natalie: Podany wykres funkcji f(x) przekształć aby uzyskać funkcję g(x) = f(x−2) h(x) = f(x) + 3 r(x) = f(−x) p(x) = −f(x)

Natalie: zna ktos rozwiazanie

Natalie: czy to zadanie ma jakies rozwiazanie? help

iza: g(x) musisz przesunąć o 2 jednostki w prawo h(x) 3 jednostki w dórę a reszta to nie wiem

iza: https://matematykaszkolna.pl/strona/1450.html masz link do tych 2 ostatnich

robinka: aby uzyskać r(x) musisz tą funkcje przekształcić względem osi OY (tzn. argumenty zmienią się na przeciwne, a wartości zostaną takie same), aby otrzymać p(x) musisz przekształcić względem osi OX(argumentu zostaną takie same, a wartości zmienią się na przeciwne)

Natalie: Dziękuje za pomoc jesteście the best

Gustlik: Przesuwanie wykresu robie wg następującego wzoru: y=f(x−p)+q → odczytuję współczynniki p i q, metodę wziąłem z postaci kanonicznej funkcji kwadratowej, aby ujednolicić tę regułę, bo dziala ona tak samo na wszystkich typach funkcji. Współczynnik p odczytuję ze zmianą znaku, współczynnik q − bez zmiany znaku i przesuwam wykres o p jednostek w poziomie i o q jednostek w pionie. Np. g(x) = f(x−2) p=2, q=0 → czyli o 2 w prawo h(x) = f(x) + 3 p=0, q=3 → czyli o 3 w górę r(x) = f(−x) → symetria wzgledem osi OY p(x) = −f(x) → symetria wzgledem osi OX.