zad
kolka: maszyna zawiera dwa koła zębate jedno ma 36 zębów a drugie 48 ie obrotow musi wykonac kazde z
tych kol aby te same zeby znow sie spotkaly
16 kwi 14:36
Jack: NWW(36,48)=...
16 kwi 14:38
kolka: 144?
16 kwi 14:43
Jack: może.... nie liczyłem. Chyba masz rację (36*4, 48*3).
16 kwi 14:44
kolka: 4Ix+3I−Ix+3I≤6:A x nalezy do R
y=2y−1/y+2>0 :B y nalezy do R
przedstaw w ukladzie wsp. AxB
16 kwi 14:52
kolka: y=2y−1 przez y+2
16 kwi 14:52
kolka: b mi wyszlo (−∞ −2) suma (2 ,∞)
16 kwi 14:53
kolka: a A nie umiem
16 kwi 14:53
Jack: nie no, moduły? Już Ci napisałem, że pierwsze musi się obrócić 4 razy ,a drugie 3.
16 kwi 14:56
Jack: nowe zadanie... ok

16 kwi 14:56
kolka: tak

16 kwi 14:57
Jack: w a) rozpisz moduł z definicji.
16 kwi 14:57
kolka: a nie moge podzielic na 4?
16 kwi 14:57
Jack: możesz ale coś Ci to da?
16 kwi 14:58
Jack: inaczej...
16 kwi 14:58
Jack: faktycznie nie musisz rozpisywać modułu ale najpierw je od siebie odejmij
16 kwi 14:59
Jack: potem podziel na 3 i odczytaj przedział z |x−a|≤b jako odległość punktu a od b o nie więcej niż
b .
16 kwi 14:59
kolka: aha czyli 3Ix+3I≤6 i teraz na 3Z?
16 kwi 15:00
kolka: a B?
16 kwi 15:01
Jack: tak, czyli będzie |x+3|≤2 i to juz można interpretować nie rozpisując modułów.
16 kwi 15:02
Jack: | | 2y−1 | | 2(y+2)−5 | |
w b) przedstaw |
| = |
| =...
|
| | y+2 | | y+2 | |
Określ dziedzinę. Zauważ że będzie to pewna funkcja hiperboliczna przesunięta o wektor...
16 kwi 15:03
kolka: ale ja mam to dac w postaci iloczynu i ja po prostu pomnozylam licznik i mianownik
16 kwi 15:04
kolka: wyznaczylam pierwiastki walnelam parabolke i odczytalam
16 kwi 15:04
kolka: dobra mneijsza o to a to IxI−2
−−−−−−−−−≤0 i wyszlo mi 2 przypadki i ogolnie suma mi wyszla
od (3 do∞) spr to
x2−3x
16 kwi 15:06
Jack: jasne... to nierówność − nie zauważyłem.
16 kwi 15:08
16 kwi 15:08
kolka: tak jest
16 kwi 15:10
kolka: i wyszlo mi z 1 przypadku x<o,2> suma<3 ∞) i z drugiego i tu nie jestem pewna (−2,0)suma(3 ∞)
16 kwi 15:11
Jack: mi wyszło <−2,0)
16 kwi 15:13
Jack: w pierwszym (−∞,0> u (2,3). Weź to, co pod osią.
16 kwi 15:14
kolka: a mozesz rozpisac 2 przypadki znaczy chodzi mi o wyniki 2 przypadkow
16 kwi 15:14
Jack: drugie też mi tak wyszło jak Tobie.
16 kwi 15:14
kolka: no ale zaczynales od dolu rysowac tak9zaczynam od lewej)
16 kwi 15:14
kolka: no ale nie ma byc nierownosc (x−2)x(x−3)≥0?
16 kwi 15:15
kolka:
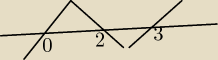
pot
16 kwi 15:16
kolka: a juz widze
16 kwi 15:20
kolka: dzieki
16 kwi 15:21
Jack: nie zmieniłem znaku nierówności, a rys. ten sam
16 kwi 15:21
kolka: czyli masz dobrze czy ja mialm dobrze

16 kwi 15:21
kolka: hm?
16 kwi 15:23
Jack: wiec po rozpisaniu powinno wyjść <−2,0) u <2,3)
16 kwi 15:23
kolka: cholera jasna
16 kwi 15:24
Jack: można rozpisywać moduły na różne sposoby, ja skorzystałem z def. i na pewno dobrze zrobiłem
(zrobiłem rys i się zgadza). Ty nie wiem z czego korzystałaś zmieniając znak.
16 kwi 15:25
kolka: skad to masz

16 kwi 15:25
Jack: ok, napiszę to

16 kwi 15:25
kolka: mi ogolnie wyszlo <−2,0>
16 kwi 15:25
kolka: juz nie trzeba nei mam czasu
16 kwi 15:25
Jack: Dziedzina x∊R\{0,3}
rozpisz moduł
x dla x≥0
−x dla x<0
Potem zbieraj wyniki z pierwszego Ci wyjdzie że x∊ (−∞,0) u <2,3>, ale biorąc warunki zostanie
<2,3)
W drugim przypadku wyjdzie, że x∊ <−2,0> u <3,∞), czyli po warunkach, że <−2,0).
Odp to suma tych przedziałów.
16 kwi 15:30


 pot
pot


