 pokazcie jak to sie robi
zad1. Suma przedziałów (−∞,10} u {10,+∞) jest zbiorem rozwiązan nierownosci.
a) |x|<10
b)|x|≤10
c) |x|>10
d) |x|≥10
zad2
Równanie x2=4 jest rownowazne rownaniu
a) x=4
b) x=0
c) x(x+4)=0
d) x(x−4)=0
zad3
Funkcja f(x) = (13 m−6) x+2 nie ma miejsc zerowych dla
a) m=18
b)m=2
c) m=−2
d) m=−18
zad4. kąt ostry α jest wiekszy od kata ostrego β. Wynika ze
a) sin β <sinα
b) cos β<cosα
c) tgβ>tgα
d) tgβ<cosα
pokazcie jak to sie robi
zad1. Suma przedziałów (−∞,10} u {10,+∞) jest zbiorem rozwiązan nierownosci.
a) |x|<10
b)|x|≤10
c) |x|>10
d) |x|≥10
zad2
Równanie x2=4 jest rownowazne rownaniu
a) x=4
b) x=0
c) x(x+4)=0
d) x(x−4)=0
zad3
Funkcja f(x) = (13 m−6) x+2 nie ma miejsc zerowych dla
a) m=18
b)m=2
c) m=−2
d) m=−18
zad4. kąt ostry α jest wiekszy od kata ostrego β. Wynika ze
a) sin β <sinα
b) cos β<cosα
c) tgβ>tgα
d) tgβ<cosα
 zad 1)
|x|≥10
x≥>=10 lub x≥<=−10
wiec x ∊(−∞,−10} u {10,+∞)
zad 1)
|x|≥10
x≥>=10 lub x≥<=−10
wiec x ∊(−∞,−10} u {10,+∞)
| 1 | |
m−6=0 | |
| 3 |
 Uwaga do Łukasza − nie rysuje się strzałek, które Ty zaznaczyłeś, a nawet uważa się za
błąd rysowanie strzałek w lewo, bo liczby na osi rosną w prawą stronę. Natomiast trzeba
zaznaczyć strzałkę na samej osi liczbowej.
Nie trzeba zamalowywać kółeczek przy przedziałach domkniętych, lepiej jest wyraźnie zaznaczyć,
położenie kółeczka, po lewej lub po prawej stronie pionowej kreseczki.
Uwaga do Łukasza − nie rysuje się strzałek, które Ty zaznaczyłeś, a nawet uważa się za
błąd rysowanie strzałek w lewo, bo liczby na osi rosną w prawą stronę. Natomiast trzeba
zaznaczyć strzałkę na samej osi liczbowej.
Nie trzeba zamalowywać kółeczek przy przedziałach domkniętych, lepiej jest wyraźnie zaznaczyć,
położenie kółeczka, po lewej lub po prawej stronie pionowej kreseczki.
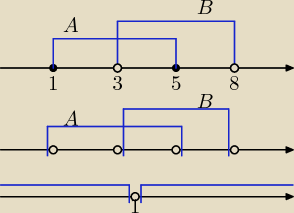 Nie sprawdza się świetnie metoda z zamalowywaniem kółeczek, szczególnie przy wyznaczaniu
różnicy przedziałów, wyjaśnię to na przykładzie.
Zadanie.
Wyznaczyć A \ B oraz B \ A, jeśli A = <1, 5>, B = (3, 8).
Rozwiązanie metodą z zamalowaniem kółeczek − tu często (wiem to z wieloletniego sprawdzania
prac) uczeń automatycznie przyjmuje liczbę przy zamalowanym kółeczku jak koniec przedziału
domkniętego i pisze takie odpowiedzi:
A \ B = <1, 3), B \ A = <5, 8)
Rozwiązanie bez zamalowywania kółeczek − tu widać wyraźnie, która liczba w którym przedziale
jest domknięta.
A \ B = <1, 3>, B \ A = (5, 8)
Wyraźnie również można zaznaczyć np.: x ≠ 1
Nie sprawdza się świetnie metoda z zamalowywaniem kółeczek, szczególnie przy wyznaczaniu
różnicy przedziałów, wyjaśnię to na przykładzie.
Zadanie.
Wyznaczyć A \ B oraz B \ A, jeśli A = <1, 5>, B = (3, 8).
Rozwiązanie metodą z zamalowaniem kółeczek − tu często (wiem to z wieloletniego sprawdzania
prac) uczeń automatycznie przyjmuje liczbę przy zamalowanym kółeczku jak koniec przedziału
domkniętego i pisze takie odpowiedzi:
A \ B = <1, 3), B \ A = <5, 8)
Rozwiązanie bez zamalowywania kółeczek − tu widać wyraźnie, która liczba w którym przedziale
jest domknięta.
A \ B = <1, 3>, B \ A = (5, 8)
Wyraźnie również można zaznaczyć np.: x ≠ 1
 (choć przypuszczam, że rysując jakiś wykres w układzie współrzędnych i zaznaczając miejsca
zerowe, niektórzy uczniowe mogą się zastanawiać czy przepuścić prostą przez miejsce zerowe,
czy tuż obok. A wyznaczając przedziały na wielomianów wyższych stopni, nie wiedzieć w końcu
jaki przedział jest właściwy. A potem jak liczbą granice prawostronne czy lewstronne to mogą
się gubić, nie wiedzieć czy wartość będzie 0+ czy 0−)
(choć przypuszczam, że rysując jakiś wykres w układzie współrzędnych i zaznaczając miejsca
zerowe, niektórzy uczniowe mogą się zastanawiać czy przepuścić prostą przez miejsce zerowe,
czy tuż obok. A wyznaczając przedziały na wielomianów wyższych stopni, nie wiedzieć w końcu
jaki przedział jest właściwy. A potem jak liczbą granice prawostronne czy lewstronne to mogą
się gubić, nie wiedzieć czy wartość będzie 0+ czy 0−)