ktora z prostych jest styczna do okregu aga: ktora z prostych jest styczna do okregu x²+y²=4x x=−2 y=2 x=−4 y=4 jak to sie robi

Godzio: x² − 4x + 4 + y² = 4 (x−2)² + y² = 4 S(2,0) r = 2 np. odleglosc środka od prostej A x = −2 d = r x = − 2 0*y + 1*x + 2 = 0 S(2,0)

	|0*2 + 0*1 +2|
d =		= 2
	√02+12

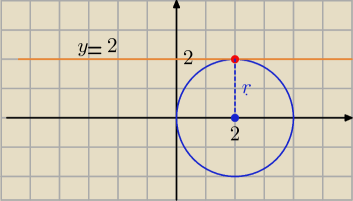
mix: Ponieważ zadanie jest z grupy zadań testowych ( zamkniętych) wystarczy ,że narysujesz ten okrąg i wszystko będzie jasne : o: x²+y²=4x => x²−4x +4 −4 +y²=0 => ( x−2)² +y²= 4 to: S( 2,0) r= 2 odległość "d" środka S od prostej y = 2 jest d=r=2 więc prosta y=2 jest styczna do tego okręgu poprawna odp: b)

Godzio: No tak pomyliłem kolejność x + 0y + 2 = 0 ...

mix: styczną jest też oś OY , ale nie ma propozycji takiej odp

aga: dzieki ale skad sie wzielo to pierwsze przeksztalcenie: x²−4x +4 −4 +y²=0

mix: Tak sprowadza się równanie okręgu do postaci kanonicznej (środkowej) by wyznaczyć współrzędne środka i dł. promienia okregu Powinnaś to znać ........

aga: wlasnie ....nic nie pamietam ale dzieki za pomoc, juro sie za to wezme

aga: prosze o pomoc...rozumiem ze korzystamy ze wzoru na rownanie okregu ....w zadaniu zostalo przeniesione 4x na lewa strone i...co dalej....dopisujemy +4 i − 4 zeby skorzystac ze wzoru skroconego mnozenia?

Basia: x²+y²=4x x²−4x+y²=0 (x−2)²=x²−4x+4 ⇒ x²−4x=(x−2)²−4 (x−2)²−4+(y−0)²=0 (x−2)²+(y−0)²=4 stąd: S(2;0) r²=4 ⇒ r=2

aga: dzieki Basia, czyli odejmujemy 4 bo potrzebujemy (x−2)² a tak wychodzi ze wzoru skroconego mnozenia?