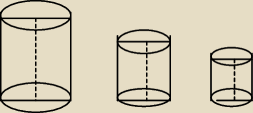
Pomocy! Ana02: Pomóżcie. Przekroje osiowe trzech walców przedstwaionych na rysunkach są kwadratami, których pola (w cm2) sa kolejnymi wyrazami ciągu geometrycznego o ilorazie 1/4. Pole powierzchni całkoitej największego walca jest równe 24π cm2. Oblicz objętości największego i najmniejszego z walca.

aga: Pc=2π*r²+2π*r*H Pc=24π stąd 2π*r²+2π*r*H=24π /:2π r²+r*H=12 skoro przekroje osiowe to kwadraty , to H=2r podstawmy do poprzedniego równania r²+r*2r=12 3r²=12 r=2 dalej H=4 największy walec ma V=π*2²*4=16π

aga: P największego przekroju osiowego=4*4=16

	1
najmniejszego więc to 16*(		)2=1
	4

stąd H=1 a promien r=0,5 V już obliczysz