matura Jagoda: zad maturalne Dana jest prosta l o rownaniu y=3x−1 oraz punkt A=(6,2) wyznacz punkt B symetryczny do punktu A wzgledem prostej l

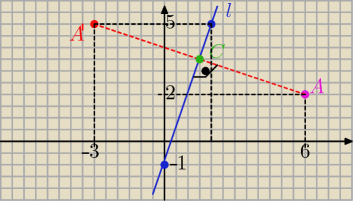
y.z.: l : y= 3x−1 wsp. kier. a₁= 3 prosta: AC prostopadła do l ma równanie: AC: y= −¹₃( x −x_A) + y_A AC: y= −¹₃( x −6)+2 = −¹₃x +4 rozwiązując układ równań prostych l i AC otrzymujemy punkt C ,który jest środkiem odcinka AA^' y= 3x −1 y= −¹₃x+4 => x= 1,5 i y= 3,5 C( 1,5 ; 3,5)

	xA+xA'		yA+yA'
zatem: xC=		i yC=
	2		2

to: x_A^'= 2x_C −x_A i y_A^'= 2y_C − y_A x_A^'= 3 −6 = −3 i y_A^'= 7−2=5 odp: A^'( −3, 5)