:))) julia : Przekrojem osiowym stozka jest trojkat rownoramienny o kacie miedzy samionami 120 stopni. Oblicz pole powierzchni calkowitej tego stozka, wiedzac ze jego objetosc jest rowna 27π cm³

Anna: Pomogę.

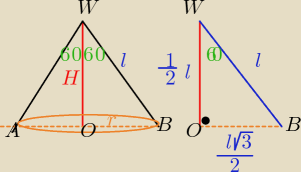
y.z.: Δ OBW −− jest połówką trójkąta równobocznego o boku długości "l" więc:

	1
H=		l
	2

	l√3
r=
	2

	1		1		3l2		1		l3*π
V=		πr2*H=		π*		*		l=
	3		3		4		2		8

l3π
	= 27π
8

l³= 8*27 => l= 2*3=6

	6√3
l=6 , H= 3 , r=		= 3√3
	2

P_c= πr³+πrl=..........

y.z.: Sorry: P_C= πr²+πrl =......

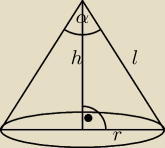Anna: α= 120⁰, V = 27π cm³, P_c = ? P_c = πr² + πrl

	1
V =		πr2h
	3

	1
		πr2h = 27π
	3

	1
		r2h = 27 ⇒ r2h = 81
	3

	r		α
		= tg
	h		2

	r
		= tg600
	h

	r
		= √3 ⇒ r = h√3
	h

Po podstawieniu: (h√3)² * h = 81 3h³ = 81 /:3 h³ = 27 ⇒ h = 3 cm r = 3√3 cm

	r		α
		= sin
	l		2

	3√3		√3
		=
	l		2

l√3 = 6√3 ⇒ l = 6 cm P_c = π*(3√3)² + π*3√3*6 = 27π + 18√3π = 9π(3 + 2√3)[cm²]