trójkąt abc jest wpisany w okrag o promieniu r . w trojkacie tym ab= 10 bc=13 ka krystian prosi o pomoc: trójkąt abc jest wpisany w okrag o promieniu r . w trojkacie tym ab= 10 bc=13 kat abc=120stopni a)oblicz dlugosc boku ac b)wyznacz peomien tego okregu

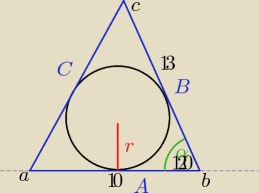
e: ac=?=C r=2P/A+B+C − promień w okręgu wpisanym w trójkąt P=1/2 AB sinα= 1/2*10*13*sin120=1/2*130*^√3₂=65*^√3₂ W dowolnym trójkącie kwadrat dowolnego boku jest równy sumie kwadratów pozostałych boków, pomniejszonej o podwojony iloczyn tych boków i cosinusa kąta zawartego między nimi. C²=A²+B²−2*A*B*cosα C²=100+169−260*(−¹₂)=269+130=399 C=√399=19,97≈20 h=√B²−(1/2A)²=√169−25=√144=12 P=1/2A*h=1/2*10*12=60 r=2*60/10+13+20=120/43=2,79≈2,8 ac≈20 r≈2,8 Mam nadzieję ze nie walnęłam się w obliczeniach

Bogdan: Zazwyczaj dużymi literami oznacza się punkty, a więc i wierzchołki figur, a małymi literami oznacza się długości odcinków, np. boków trójkąta. Jednak e walnęłaś się, bo trójkąt ABC jest wpisany w okrąg, a nie jest opisany na okręgu.

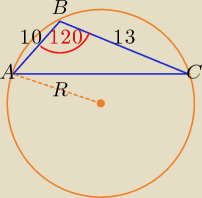
Bogdan: Przy wyznaczeniu |AC| korzystamy z twierdzenia cosinusów. Długość promienia R okręgu wyznaczymy stosując twierdzenie sinusów:

|AC|
	= 2R
sin120o

e: Bogdanie ależ wiem ze jest taki zwyczaj ale krystian użył innych.... No i dzięki umknęło mi w wirze rozwiązywania rzeczywiście wpisany a nie oisany No to zrobiłam zupełnie inne zadanie