romb Hania =): Połączono środki boków rombu. Wykaż, że otrzymany czworokąt jest prostokątem.

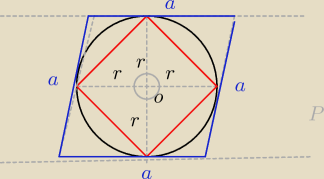
e: Środek przekątnych, które przecinają się pod kątem prostym, jest środkiem okręgu (o) wpisanego w ten romb o bokach = a. Promień okręgu wpisanego = r. Promienie okręgu tworzą z bokiem czworokąta trójkąt równoramienny prostokątny o ramionach równych r. Powstały 4 takie same trójkąty w których ich przeciwprostokątne tworzą czworokąt. Każdy trójkąt prostokątny i równoramienny, stąd kąty przy ramionach trójkątów = (80−90):2=45, no i są takie same. Stąd każdy kąt powstałego czworokąta ma złożony z 2 kątów trójkąta; taki sam równy 45*2=90− kąt prosty. No i mamy prostokąt jest także kwadratem.

Hania =): to czerwone mi wyszło na rysunku jako prostokąt..

Wydi: kwadrat jest prostokątem

Hania =): ale prostokąt nie jest kwadratem

e: To coś z rysunkiem nie tak. ROMB ma boki równe. Przekątne "kawdratu czerwonego" takie same bo ich długości równe 2 x promień okręgu wpisanego w romb. Jak sobie policzysz to wszystkie boki "kawdratu" równe bo przyprostokątne trójkątów równe. Wynoszą r√2