

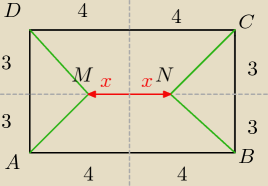
 |BN|2=|CN|2=|AM|2=|DM|2=(4−x)2+32
Zatem 4*[ (4−x)2+32 ] + (2x)2 =F(x)
Trzeba zwyczajnie policzyć wierzchołek paraboli F(x).
Potem to co wyjdzie należy pomnożyć przez 2 aby otrzymać długość odcinka MN (czyli odległość
punktu M od N).
|BN|2=|CN|2=|AM|2=|DM|2=(4−x)2+32
Zatem 4*[ (4−x)2+32 ] + (2x)2 =F(x)
Trzeba zwyczajnie policzyć wierzchołek paraboli F(x).
Potem to co wyjdzie należy pomnożyć przez 2 aby otrzymać długość odcinka MN (czyli odległość
punktu M od N).
| x | ||
(można było od razu nazwać przez | to co nazwałem przez x − kwestia gustu. Ale mam | |
| 2 |
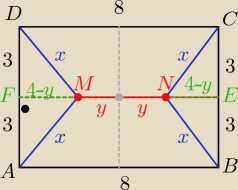 IMNI= 2y INEI=IMFI= 4−y IAMI=IDMI=IBNI=ICNI= x
to: 4x2+(2y)2 −−− ma osiągać minimum
z ΔAMF z tw. Pitagorasa mamy:
x2= (4−y)2+32 = y2 −8y +25
to: f(y) = y2−8y+25+ 4y2 = 5y2 −8y+25 −−− to f. kwadratowa , osiąga minimum
IMNI= 2y INEI=IMFI= 4−y IAMI=IDMI=IBNI=ICNI= x
to: 4x2+(2y)2 −−− ma osiągać minimum
z ΔAMF z tw. Pitagorasa mamy:
x2= (4−y)2+32 = y2 −8y +25
to: f(y) = y2−8y+25+ 4y2 = 5y2 −8y+25 −−− to f. kwadratowa , osiąga minimum
| 8 | ||
dla ymin= | = 0,8
| |
| 2*5 |