| a+b | ||
Wykaż, że odcinek x łączący środki ramion trapezu o podstawach a,b ma długość | ||
| 2 |
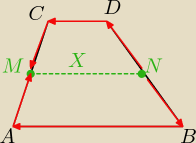 → → → →
x = NB +BA +AM wektory ND i NB sa takiej samej dl kierunku
ale przeciwnym zwrocie wiec sumach ich wynosi wektor 0 tak samo z AM i CM sym. ND=−NB
AM=−CM
→ → → →
x = ND + DC+ CM
→ → → → → → →
2x = NB −NB +AB+AM −CM+ CD
→ → →
2x = AB +CD
→ →
AB=a CD=b
2x=a+b
→ → → →
x = NB +BA +AM wektory ND i NB sa takiej samej dl kierunku
ale przeciwnym zwrocie wiec sumach ich wynosi wektor 0 tak samo z AM i CM sym. ND=−NB
AM=−CM
→ → → →
x = ND + DC+ CM
→ → → → → → →
2x = NB −NB +AB+AM −CM+ CD
→ → →
2x = AB +CD
→ →
AB=a CD=b
2x=a+b
| a+b | ||
x= | ||
| 2 |

 ok
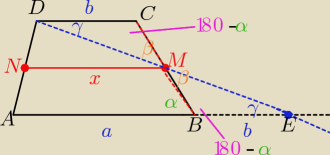
ok Podaję inny dowód ( bez wykorzystania wektorów)
ΔBEM przystaje do ΔCDM z cechy ( k,b,k)
zatem: IBEI=IDCI= b
IAEI= a+b
w Δ AED odcinek x łączy środki boków AD i DE
więc jest równoległy do boku AE i jego długość równa jest połowie
długości IAEI
Podaję inny dowód ( bez wykorzystania wektorów)
ΔBEM przystaje do ΔCDM z cechy ( k,b,k)
zatem: IBEI=IDCI= b
IAEI= a+b
w Δ AED odcinek x łączy środki boków AD i DE
więc jest równoległy do boku AE i jego długość równa jest połowie
długości IAEI
| a+b | ||
zatem: x= | ||
| 2 |
 bo w troj AED odrazu wzioles ze ten odcinek jest polowa
podstawy trojkata a tak nie mozna chyba, bo dowod sredniej arytmetycznej przeprowadzasz
wlasnie
bo w troj AED odrazu wzioles ze ten odcinek jest polowa
podstawy trojkata a tak nie mozna chyba, bo dowod sredniej arytmetycznej przeprowadzasz
wlasnie 