help! Wydi: W trójkącie o obwodzie 14 jeden z boków jest dwa razy dłuższy od drugiego. Oblicz cosinus najmniejszego kąta tego spośród trójkątów spełniających podany warunek, w którym suma kwadratów długości boków jest najmniejsza.

Wydi:

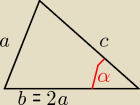
y.z.: a, b, c −−− dł. boków , a,b, c >0 b= 2a a+2a+c= 14 => 3a +c= 14 => c = 14 − 3a , dla a€ (0, ¹⁴₃) a²+(2a)² +c² = 5a² +c² −−− ma mieć minimum f(a)= 5a²+(14−3a)² = 14a² −84a +196 −−− f. jest kwadratowa , ramiona paraboli do góry zatem f(a) osiaga minimum dla

	84
amin=		= 3
	28

zatem b_min= 2*3= 6 i c_min = 14−3*3= 5 trójkąt ma boki długości: a= 3 , b= 6 , c= 5 najmniejszy kąt α −−− na przeciw najkrótszego boku ze wzoru cosinusów:

	b2+c2−a2		50		5
cos α=		=		=
	2bc		60		6

Wydi: Dziękuje y.z

magggg: b²+c²−a² = 6²+5²−3² = 36+25−9 = 52 tak na mój rozum, czyli wynik to ⁵²₆₀