;( Maciek: Z wycinka kołowego o powierzchni 72π i promieniu 12 zwinięto powierzchnię boczną stożka. Oblicz jego objętość.

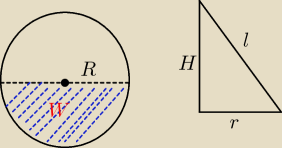Tomek.Noah: R=12 P_{wycinka kola}=72π Sz: V−obijetosc stozka potrzbene H i r_podstawy Pole wycinka kola:

	α
P=		* πR2
	360o

	360o * P
α=
	πR2

	360o * 72π
α=
	π * 144

	1
Skoro alfa wynosi 180o to wiem ze obwod podsatwy jest rowny		obodu kola z ktorego ten
	2

wycinek zostal wyciety

	1
Op=		Ok
	2

	1
Op=		* 24π
	2

O_p=12π Skoro obowd podstawy stozka wynosi 12π to obliczmy promien tej podstawy ktory jest nam potrzebny do V 12π=2πr r=6 Brakuje nam H ale jezeli sie przyjzec wycinkowi na okregu to widzimy ze l=R zatem z tw. Potagorasa mozna latwo to H obliczyc tw. Pitagorasa: a²+b²=c² H²+r²=l² H²=l²−r² H²=12²−6² H²=108 H=√108

	1
V=		πr2H
	3

	1
V=		π36*√108
	3

V=12√108π