Naszkicuj wykres funkcji g. Basia: Funkcja f(x)=|x+2| określona jest dla x ε<−1;4>. Naszkicuj wykres funkcji g. Podaj jej dziedzinę i zbiór wartości. a)g(x)=f(3x)

Jack: 1) narysuj wykres f(x)=|x| 2) przesuń go o wektor [−2,0] a) podpowiem, że wartości się nie zmienią w stosunku do f(x), ale możesz sobie narysować tę funkcję f(3x)

Basia: Ale jak przesunę to przecież wartości zmienią się w stosunku do f(x), więc nie wiem, jak mam to zrobić.

Jack: podstaw za x=3x do równania f(x)=|x+2| i napisz równianie f(3x)=...

Basia: f(3x)=|3x+2| Ale jak to będzię wyglądało na wykresie, co onacza ta 3 przed x?

Jack: Teraz mozesz już rozpisać to z definicji. 3 przed oznacza że funkcja będzie nieco ostrzej szła w górę (lub dół) w stosunku do |x+2|. Spróbuj z definicji rozpisać.

Jack: { 3x+2 dla 3x+2≥0 ⇒ x∊<−²₃,∞) g(x)=|3x+2|={ −3x−2 dla 3x+2<0 ⇒ x∊ (−∞,−²₃)

Basia: Bardzo dziwny wyszedł mi wykres, bo nie spełnia warunków zadania, ponieważ na moim wykresie x nie należy do przedziału <−1;4>.

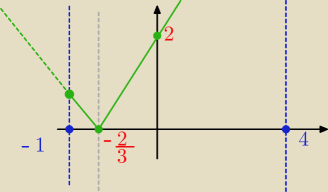
Jack: Rozwiązaniem jest ciągła zielona linia., która z prawej strony idzie aż do prostej x=4.

Basia: Dlaczego −²₃ − skąd to się wzięło. W tym zadaniu trzeba zastosować funkcję y=f(k*x), ponieważ to zadanie dotyczy tego tematu, więc chyba trzeba pomniejszyć 3 razy − tak mi się wydaje, ale nie umiem niestety tego zrobić.

Basia: Mógłbyś mi to wyjaśnić i pomóc, bo miałam z tego dopiero 1 lekcję i nie za bardzo zrozumiałam.

Jack: −²₃ wzięło się z rozpisania modułu... Tak naprawdę wszystko co narysowałem wzięło się stąd. Miałaś moduły?

Basia: Nie miałam

Basia: Więc w jaki sposób mam to zrobić?

Jack: hmm To w takim razie wyobraź sobie, że masz y=3x+2. Umiesz to narysować. Moduł nałożony na g(x) czyli g(x)=|3x+2| sprawia, że ta część która (tu: y=3x=2) znajdowała się poniżej osi, odbija się symetrycznie od OX.

Basia: Podobne zadania obliczliśmy z funkcji y=f(k*x), ale były to proste przykłądy, a ten sprawia mi spory problem.

Basia: Dlaczego to w taki sposób liczysz, przecież ten wykres to chyba trzeba pomniejszyć.

Jack: jak to "pomniejszyć"?

Basia: Z podręcznika: Funkcja y=f(k*x) − trzeba ją przekształcić poprzez zmianę jednostki na osi x w skali ¹_k

Jack: o kurde... nigdy w życiu nie przyszłoby mi do głowy żeby tak to robić... po prostu narysuj funkcję y=3x+2 − to umiesz na pewno narysować (nie potrzebujesz żadnej skali ani zmiany jednostek), a potem kawałek poniżej osią OX odbij jak w lustrze (symetrycznie).

Basia: Niestety nadal nic nie rozumiem − dlaczego mam odbijąć pod osią symetrycznie − na lekcjach żadnego odbijania nie robiliśmy − wykres po przekształceniach stawał się po prostu szerszy lub węższy od pierwotnego.

Jack: a miałaś moduły na lekcjach?

Basia: Miałeś już wykresy funkcji y=f(k*x), czy nie?

Basia: Modułów żadnych NIE MIAŁAM − nie wiem co to w ogóle jest

Basia: To zadanie jest z działu o przekształceniach wykresów funkcji, a nie o funkcji liniowej z wartością bezwzględną.

Basia: Ja naprawdę nie wiem co to są moduły − nigdy o czymś takim nie słyszałam

Basia: POMOŻESZ

Jack: gdziekolwiek to zakwalifikować, pojawia się moduł, czyli wartość bezwzględna. Nic nie pomoże intuicja dotycząca pomniejsza czy poszerzenia funkcji postaci g(x)=f(k*x)... Mozesz zerknąć tu: https://matematykaszkolna.pl/strona/1651.html

Jack: ale masz je zrobić.. moduł to nie to samo co zastosowanie zmiany skali i jednostki dla funkcji postaci y=f(k*x).

Basia: Niestety dalej nie wiem jak po narysowaniu to przekształcić i określić dziedzinę i zbiór wartości

Basia: Nie wiem na jakiej podstawie to przeksztać, czy też ,,odbijać symetrycznie"

Jack: ok, a umiesz narysować wykresy: y=3x+2 oraz y=−3x−2 na jednym układzie współrzędnych?

Basia: Umiem

Jack: to narysuj i wybierz te kawałki które lezą nad osią OX.