ostrosłupy mała: Pomóżcie proszę Pole ściany bocznej ostrosłupa prawidłowego trójkątnego jest równe a²√6 / 8, gdzie a oznacza długość krawędzi podstawy tego ostrosłupa. Oblicz cosinus kąta β, jaki ściana boczna ostrosłupa tworzy z płaszczyzną jego podstawy. Miarę kąta β podaj z dokładnością do 10

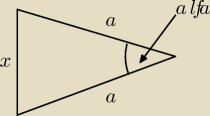
b.: dość skomplikowane to mi się wydaje proponuję zacząć od policzenia długości boku podstawy x mamy taki trójkąt (ścianę boczną) −− rysunekl pole tego trójkąta wynosi a²sin(α)/2 = a²√6/8, skąd można wyliczyć kąt α, a potem x... [stokrotka]

jedigrom: czekaj, liczę, daj mi kwadrans

jedigrom: w ogóle to rysunek jest zły, bo skoro to ma być ta ściana boczna, no to oznacz krawędź podstawy sobie jako a, tak jak w treści zadania, a długość krawędzi bocznej niech będzie x

jedigrom: β=20 stopni jak liczyłem: najpierw przyrównujesz pole które masz dane: a₂√6 / 8 = 1/2ah gdzie h jest wysokością ściany bocznej, a a jest krawędzią podstawy (podstawa to trójkąt równoboczny, przypominam) wyliczasz z tego h i ci wychodzi, że h=a √6/8 cosinus β to tak naprawdę stosunek 1/3 wysokości podstawy trójkąta równobocznego do wysokości ściany bocznej, co właśnie policzyliśmy. Weź sobie wysokość trójkąta równobocznego ze wzoru, przemnóź razy jedna trzecia, no i ten stosunek to wygląda tak: cosβ = a √3/6 dzielone przez a √6/8. Wychodzi ten cos = 2/3 √2 Pewny nie jestem

b.: rzeczywiście, źle zrobiłem rysunek i źle zacząłem, ale rozwiązanie jedigrom(a?) jest w zasadzie poprawne −− chociaż chyba wychodzi h=a√6/4 itd...

mała: dzięki ale czy można trochę jaśniej bo ja naprawdę nie rozumiem i nie wiem nadal jak to zrobić i jak powinien wyglądać rysunek

mała: dzięki ale czy można trochę jaśniej bo ja naprawdę nie rozumiem i nie wiem nadal jak to zrobić i jak powinien wyglądać rysunek

mała: do h to wiem jak liczyc ale dalej juz nie nie wiem skąd się wzięło cos 2/3√2 i ze β=20⁰ prosze o wyjaśnienie

mała: