Sprawdź czy punkty leżą na jednej prostej Damian: Sprawdź czy punkty A=(2,5), B= (4,9), C= (46,93) leżą na jednej prostej?

Eta: https://matematykaszkolna.pl/forum/46577.html

filip: y=ax+b 5=2*2+b y=ax+b 5=2a+b −b=−1/*−1 93=2*46+1 9=4a+b/*(−1) b=1 93=93 5=2a+b odp.Punkty leża na jednej prostej −9=−4a−b −4=−2a 2a=4/;2 a=2

Bogdan: Wyznaczanie równania prostej jest zbędne, wystarczy oblicz dwa współczynniki kierunkowe,

	4		88
np. prostej AB i prostej AC: aAB =		= 2, aAC =		= 2 = aAB
	2		44

a więc punkty są współliniowe

Bogdan: poprawiam chochlika: wystarczy obliczyć

pigor: ..., lub np. AB^→= [2,4] i AC^→= [44,88]= 22 [2,4] − wektory równoległe, więc 3 dane punkty są współliniowe . ...

maniek: a ja tam wole narysować tylko muszę mieć durze kartki

maniek: duże* /\

Szczex: Sprawdź, czy punkty A(−1, 2), B(0.−1) i C(2, −7) leżą na jednej prostej.

123: błędne jest założenie Bogdana, mogą mieć te proste różne współczynniki b, lecz takie same "a" co sugeruje nam że mogą leżeć na jednej prostej, lecz tak być nie musi.

123: no chyba że rozważysz 3 współczynniki kierunkowe, a nie tylko 2....

ite: 123 mówimy o sytuacji, gdy dwie proste mają równe współczynniki kierunkowe i przechodzą przez ten sam punkt (chodzi o pkt A). Czy to mogą być dwie różne proste?

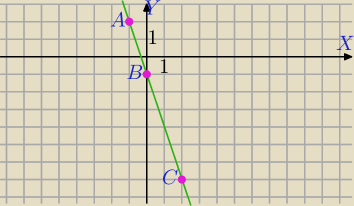
Mila: A=(−1, 2), B=(0,−1) i C=(2, −7) 1) Prosta AB: y=ax−1 i 2=a*(−1)−1 a=−3 (*) y=−3x−1 Sprawdzam, czy wsp. punktu C spełniają równanie (*) −7=^? −3*2−1 −7=−7 punkty: A,B,C są współliniowe.