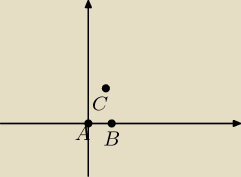
twierdzenie sinusów Karolajn: dany jest trójkąt ABC, w którym A(0.0) i B(4,0). Wyznacz współrzędne wierzchołka C, jeśli |BC|= 4√3 i kąt CAB=120 stopni.

Karolajn: up

R.W.16l: sinCAB=|BC|/|AC| sin120=√3/2 4√3/|AC|=√3/2 8√3/|AC|=√3 8√3=√3*|AC| |AC|=8 czyli √(x_C−x_A)²+(y_C−y_A)²=8 √x_C²+y_C²=8 x_C²+y_C²=64 x_C=√64−y_C² chociaż nie, chyba źle bo nie wiem co dalej, ale wyślę bo się napisałem

Bartas: ze współzednych widac ze AB=4 z twierdzenia sinusów: 4/sin120 = 4√3/sinα => α = 30 stopni jezeli trójkat to 180−30−120 = 30 => równoramienny => AB = CA " ` " − do kwadratu wzór na współżędne w zaleznosci od długości: l(długość) = √(Xa−Xb)`+(Ya−Yb)` AC` = (Xa−Xc)`+(Ya−Yc)` BC` = (Xb−Xc)`+(Yb−Yc)` − układ równań 48 = (4−x)`+(0−y)' 16 = (0−x)`+(0−y)' obustronnie razy (−1) i dodajemy stronami 32 = x`−8x+16−x` x=−2 podstawiamy do pierwszego lub drugiego równania i y z tego powinien wyjsc −2√3 v 2√3 ale nie chce mi sie pisac