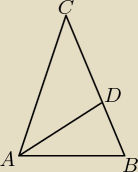 Punkt D leży na boku BC trójkąta równoramiennego ABC, w którym |AC|=|BC|. Odcinek AD dzieli
trójkąt ABC na dwa trójkąty równoramienne w taki sposób, że |AB|=|AD|=|CD| (patrz rysunek).
Oblicz miary kątów trójkąta ABC.
Punkt D leży na boku BC trójkąta równoramiennego ABC, w którym |AC|=|BC|. Odcinek AD dzieli
trójkąt ABC na dwa trójkąty równoramienne w taki sposób, że |AB|=|AD|=|CD| (patrz rysunek).
Oblicz miary kątów trójkąta ABC.
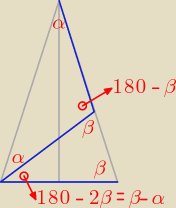 2α + 180 − β = 180 ⇒ β = 2α
180 − 2β = β − α ⇒ 180 = 3β − α ⇒ 180 = 6α − α ⇒ α = 36 i β = 72
2α + 180 − β = 180 ⇒ β = 2α
180 − 2β = β − α ⇒ 180 = 3β − α ⇒ 180 = 6α − α ⇒ α = 36 i β = 72