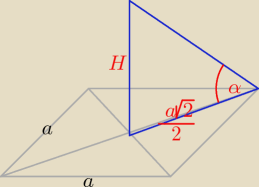
ostrosłup zimorodek: treść brzmi: Obj. ostrosłupa prawidłowego czworokątnego jest równa24 cm² a jego pole podstawy 9cm². Wyznacz miarę kąta α nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy. zrobiłam rysunek, obliczyłam że w podstawie bok wynosi a=3, wys.h=8. krawędź przypuszczam że trzeba z Pitagorasa wyliczyć: 8²* ^3√2₂ = x² (x− krawędź ostrosłupa). ale jak wyliczyć α?

rademenes:

h
	=sinα
x2

Anna: pomogę

Bogdan:

a√2     2
	= ctgα
H

Anna: Masz już rysunek, więc piszę tylko obliczenia. a= 3 cm, h = 8 cm

h
	= tgα
d   2

8
	= tgα
a√2   2

	16		16√2		8√2
tgα =		=		=
	3√2		6		3

zimorodek: Anno,a jak z tych obliczeń mogę wywnioskować miarę kąta szukanego?

Anna: Zwykle w takiej sytuacji zostawia się wynik w postaci wartości funkcji szukanego kąta, gdyż jest to wynik dokładny. Na wyraźne życzenie, można obliczyć przybliżoną wartość ostatniego ułamka i odczytać w tablicach miarę kąta. A wiesz, w jakiej postaci wynik był tu oczekiwany?

zimorodek: z pewnością wynik miał być podany w stopniach. dodam, że koleżance wyszło 75 stopni.

Anna:

	11,3137
Tak, zgadza się. tgα =		≈ 3,7712 ⇒ α ≈ 750
	3