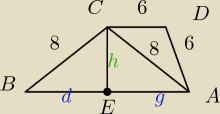
 ja bym to machnął z twierdzenia cosinusów na kąt D i zmienił go na sinus i wyliczył pole CDA i
przyrównać je do pola CDA z innego wzoru z wysokością i wyliczyć tę wysokość zeń. Ale w
sumie można wyliczyć tę wysokość z pitagorasa. ale to nam się do niczego nie przyda!
można by z pitagorasa wysokość BAC która jest równoscześnie wysokością tegoż trapezu i dzieli
poszukiwany przez nas odcinek na pół, bydzie tak :
h2+g2=82 oraz 12h*g + sin D* 6*6* 12 z tego układziku równań sobie obliczymy.
dosyć chaotycznie ale wytłumaczone. wyliczymy g, później wiemy, że 2g=AB i MAMY!
ja bym to machnął z twierdzenia cosinusów na kąt D i zmienił go na sinus i wyliczył pole CDA i
przyrównać je do pola CDA z innego wzoru z wysokością i wyliczyć tę wysokość zeń. Ale w
sumie można wyliczyć tę wysokość z pitagorasa. ale to nam się do niczego nie przyda!
można by z pitagorasa wysokość BAC która jest równoscześnie wysokością tegoż trapezu i dzieli
poszukiwany przez nas odcinek na pół, bydzie tak :
h2+g2=82 oraz 12h*g + sin D* 6*6* 12 z tego układziku równań sobie obliczymy.
dosyć chaotycznie ale wytłumaczone. wyliczymy g, później wiemy, że 2g=AB i MAMY!
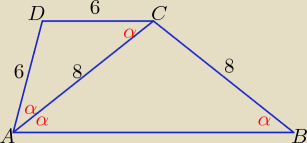 Kąty ACD i BAC są kątami naprzemianległymi, więc mają równe miary, trójkąty ACD i ABC
ze względu na równość miar odpowiadających sobie kątów wewnętrznych są trójkątami
podobnymi.
Kąty ACD i BAC są kątami naprzemianległymi, więc mają równe miary, trójkąty ACD i ABC
ze względu na równość miar odpowiadających sobie kątów wewnętrznych są trójkątami
podobnymi.
| 6 | 8 | ||
= | ⇒ |AB| = .... | ||
| 8 | |AB| |